Algorithmes utiles
Collisions
Rectangle Rectangle
Pour détecter une collision rectangle-rectangle, il faut comparer la collision en X et en Y. Il y a collision si il y a collision en X et en Y.
Par exemple en X, on a 3 cas : trop à gauche, trop à droite, et dans le dernier cas ça touche.
if le premier rectangle est totalement à gauche du deuxième:
ne touche pas
else:
if le premier rectangle est totalement à droite du deuxième:
ne touche pas
else:
touche

On continuera notre cascade de if/else en nous demandant si il est trop haut et trop bas. Ce qui nous fait 4 conditions à tester.
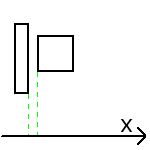
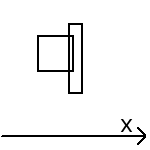
# perso (personnage) et obj (objet) sont des rectangles définis par x1, y1, x2, y2 (voir figure)
if perso.x2 < obj.x1: # perso est trop à gauche
ne touche pas
elif perso.x1 > obj.x2: # perso est trop à droite
ne touche pas
elif perso.y2 < obj.y1: # perso est trop en haut
ne touche pas
elif perso.y1 > obj.y2: # perso est trop en bas
ne touche pas
else:
touche
draw.rect pour en dessiner un.
Pour la 3D, on continuera notre cascade avec trop loin et trop proche, nous menant à 6 conditions.
Cela peut s'écrire en une seule ligne avec des or.
if perso.x2 < obj.x1 or perso.x1 > obj.x2 or perso.y2 < obj.y1 or perso.y1 > obj.y2:
ne touche pas
else:
touche
Et inverser la condition avec not.
if not(perso.x2 < objet.x1 or perso.x1 > objet.x2 or perso.y2 < objet.y1 or perso.y1 > objet.y2):
touche
else:
ne touche pas
Pour certains jeux, on traite les collisions différemment en fonction du côté de collision, par exemple dans Mario, une collision par le haut d'un ennemi le tue, alors qu'une collision par le côté tue Mario. On gardera donc la cascade de if/elif.
Point Rectangle
Pour avoir une collision point-rectangle, on peut voir le point comme un rectangle de taille zéro.
if not(perso.x2 < obj.x or perso.x1 > obj.x or perso.y2 < obj.y or perso.y1 > obj.y):
touche
else:
ne touche pas
Cercle Cercle
Pour une collision cercle-cercle, il y a collision si la distance entre les deux centres est plus petite que la somme des rayons. Pour calculer la distance entre deux points, utilisez Pythagore.
distance = pythagore(centre1X - centre2X, centre1Y - centre2Y) # = sqrt(a*a + b*b) = sqrt(a**2 + b**2)
if distance < rayon1 + rayon2:
touche
else:
ne touche pas

Remarquez que vu que la condition distance < rayon1 + rayon2 est la même que distance² < (rayon1 + rayon2)², le calcul peut se faire sans racine carrée :
dx = centre1x - centre2x
dy = centre1y - centre2y
if dx ** 2 + dy ** 2 < (rayon1 + rayon2) ** 2:
touche
else:
ne touche pas
Point Cercle
Pour avoir une collision point-cercle, on peut voir le point comme un cercle de rayon zéro.
dx = centrex - px
dy = centrey - py
if dx ** 2 + dy ** 2 < rayon ** 2:
touche
else:
ne touche pas
Cercle Rectangle
Voici le code :
# cx,cy = centre du cercle
# rx,ry = centre du rectangle
# w,h = largeur/hauteur du rectangle
hrx, hry = w/2, h/2
clampX = min(max(cx - rx, -hrx), +hrx)
clampY = min(max(cy - ry, -hry), +hry)
closestX = rx + clampX
closestY = ry + clampY
if pythagore((closestX, closestY), (cx,cy)) <= rayon:
touche
else:
ne touche pas
Ce code vient de cette page, chapitre AABB - Circle collision detection.
Remarquez que faire
y = min(max(x, m), M)
revient à faire :
y = x
if y < m: # pas plus petit que le minimum !
y = m
else:
if y > M: # pas plus grand que le maximum !
y = M
Le site learnopengl.com est un très bon tutoriel pour apprendre de l'opengl moderne (2010) et donc la programmation de shaders.
Rebond
Quand une balle (ou un rayon de lumière) rebondit sur un mur, il se passe ceci :
Angle
Une manière de voir le rebond est que l'angle change :
- Quand la balle rebondit sur le mur de droite (ou gauche), on a donc θ' = 180° − θ.
- Quand la balle rebondit sur le mur du bas (ou du haut), on a donc θ' = − θ.
On peut également trouver la formule pour quand le mur est à un angle quelquonque α. Pour le mur de droite, nous avions α = 180°, pour le mur du haut nous avions α = 270°.
Vecteur
On peut également voir ça vectoriellement, on cherche à on cherche à calculer le nouveau vecteur vitesse v'.
- Pour le mur de gauche (ou de droite), on a donc x' = − x et y' = y.
- Pour le mur du haut (ou du bas), on a donc y' = − y et x' = x.
Cas général
Le cas général, qui marche aussi en 3D, est quand le mur a un vecteur normal n, la formule sera donnée par la loi de la réflexion :
n = n / norm(n) # on normalise n, norm(n) = sqrt(n.x ** 2 + n.y ** 2)
nouveau_v = v + 2 * dot(n, v) * n # dot est le produit scalaire, dot(n,v) = n.x * v.x + n.y * v.y
Remarquez que le signe du produit scalaire présent dans la formule permet de savoir si la balle rentre dans le mur (produit négatif) ou non (produit positif), si le produit est nul, elle avance paralèlement au mur (v et n sont perpendiculaires).
En 3D, nous rebondissons bien-sûr sur un plan, les plans ont également des normales.
Afficher des entiers
Pour afficher des infos comme le nombre de vies ou les points, on a deux choix :
- Soit sous forme de nombre. Voir pygame8_texte.py et theorie2 (en savoir plus).
- Soit afficher une étoile par point gagné/vie restante. Cela fera travailler les boucles !
Supprimer correctement d'une liste
Souvent dans les jeux, on a besoin de supprimer depuis une liste des éléments selon un critère.
Par exemple, on veut supprimer toutes les pièces qui sont en contact avec le joueur, ou o aimerait enlever de la liste des joueurs tout ceux qui n'ont plus de vie.
Prenons un exemple plus simple, nous avons une liste de nombre et voulons supprimer tous les nombres plus grand que 5.
L'approche naïve ne marche pas :
L = [1,2,7,8,1,3,6,7]
i = 0
while i < len(L):
if L[i] > 5:
del L[i]
i = i + 1
La boucle sautera un élément. Je vous invite à tester le code dans pythontutor pour voir le problème.
La solution est de ne pas incrémenter le compteur quand l'élement est supprimé :
L = [1,2,7,8,1,3,6,7]
i = 0
while i < len(L):
if L[i] > 5:
del L[i]
else:
i = i + 1
Autre astuce : créer une variable pour se souvenir de la suppression.
L = [1,2,7,8,1,3,6,7]
i = 0
while i < len(L):
to_delete = False
if L[i] > 5:
to_delete = True
if to_delete:
del L[i]
else:
i = i + 1
Autre astuce un peu moins efficace mais probablement plus facile à coder, créer une corbeille :
L = [1,2,7,8,1,3,6,7]
corbeille = []
for x in L:
if i > 5:
corbeille.append(x)
for y in corbeille:
L.remove(y)
Monde infini
Cette technique est utile pour faire un monde de taille bien plus grande que la fenêtre.
Imaginez avoir un personnage (image), des pièces (cercles), des ennemis (cercles) et des batiments (rectangles), chacun ont leur classe, leur position (x,y), largeur (w), hauteur (h), rayon (r) et sont tous dans leur listes respective.
Ma fenêtre est de taille (700, 500) mais mon monde est bien plus grand.
L'approche classique est de dessiner la scène comme ceci :
# personnage
image_perso.blit(ecran, [charac.x, charac.y])
# scène
for p in liste_piece:
pygame.draw.circle(ecran, JAUNE, [p.x, p.y], p.r)
for e in liste_ennemi:
pygame.draw.circle(ecran, ROUGE, [e.x, e.y], e.r)
for b in liste_batiment:
pygame.draw.rect(ecran, BLEU, [b.x, b.y, b.w, b.h])
Je ne pourrai alors que voir les points entre (0,0) et (700,500) de mon monde.
L'idée est d'avoir une caméra qui se déplace, ici elle est en (0,0) mais si elle était en (50,100), on verrait les points de (50,100) à (750,800).
Un élément dont la position dans le monde vaut (150,270) se verrait alors dessiné sur l'écran en (100,170).
Nous devons donc dessiner tous nos éléments en (x - camera.x, y - camera.y).
# personnage
image_perso.blit(ecran, [charac.x - camera.x, charac.y - camera.x])
# scène
for p in liste_piece:
pygame.draw.circle(ecran, JAUNE, [p.x - camera.x, p.y - camera.x], p.r)
for e in liste_ennemi:
pygame.draw.circle(ecran, ROUGE, [e.x - camera.x, e.y - camera.x], e.r)
for b in liste_batiment:
pygame.draw.rect(ecran, BLEU, [b.x - camera.x, b.y - camera.x, b.w, b.h])
Pour un rpg, le plus simple est généralement qu'à chaque tick, la caméra soit sur le joueur. Nous rajouterons donc la logique suivante à chaque tick :
# la camera suit automatiquement le perso
camera.x = perso.x
camera.y = perso.y
Vu que le perso est dessiné en (perso.x - camera.x, perso.y - camera.y), le perso sera toujours dessiné en (0,0), on peut mettre la caméra un peu plus loin pour que le perso soit au milieu de l'écran (350,250) :
# la camera suit automatiquement le perso
camera.x = perso.x - 350
camera.y = perso.y - 250
La position à l'écran du perso vaudra donc (perso.x - camera.x, perso.y - camera.y) = (perso.x - (perso.x - 350), perso.y - (perso.y - 250)) = (+350, +250)
Mais libre à vous de faire une caméra plus fantaisiste ! Pour un jeu que j'ai créé, j'ai appliqué un ressort avec frottement linéaire entre la caméra et le joueur et ça donnait très bien !
# la camera suit automatiquement le perso mais avec un peu de retard
alpha = 0.80 # 80% du déplacement est pris à chaque tick
camera.x = camera.x + alpha * (perso.x - 350 - camera.x)
camera.y = camera.y + alpha * (perso.y - 250 - camera.y)
 English here!
English here!