Useful algorithms
Collisions
Rectangle Rectangle
To detect a rectangle-rectangle collision, one has to compare the collision along X and Y axe. There is a collision if there is a collision in X and Y.
For example in X, we have 3 cases : too much to the left, too much to the right, and in the last case there is a collision.
if first rectangle is totally to the left of the second:
no collision
else:
if first rectangle is totally to the right of second:
no collision
else:
collision
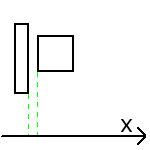

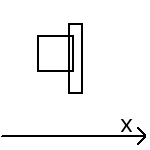
We wil continue our if/else cascade by asking if it is too much to the top and the bottom. This gives us 4 conditions to test.
# charac (character) and obj (object) are rectangles defined by x1, y1, x2, y2 (see figure)
if charac.x2 < obj.x1: # charac is too much to the left
no collision
elif charac.x1 > obj.x2: # charac is too much to the right
no collision
elif charac.y2 < obj.y1: # charac is too much to the top
no collision
elif charac.y1 > obj.y2: # charac is too much to the bottom
no collision
else:
collision
draw.rect to draw one.
In 3D, we will continue our cascade with too far and too near, this gives us 6 conditions.
This can be written with one ligne by using or.
if charac.x2 < obj.x1 or charac.x1 > obj.x2 or charac.y2 < obj.y1 or charac.y1 > obj.y2:
no collision
else:
collision
And inverse the condition with not.
if not(charac.x2 < obj.x1 or charac.x1 > obj.x2 or charac.y2 < obj.y1 or charac.y1 > obj.y2):
collision
else:
no collision
In certain games, one has to treat collisions differently depending on the side of the collision, for instance in Mario, a collision from the top by an ennemy kills it, whereas a collision from the side kills Mario. Therefore we'll keep the if/elif cascade.
Point Rectangle
To have a point-rectangle collision, we can see the point as a zero-size rectangle.
if not(charac.x2 < obj.x or charac.x1 > obj.x or charac.y2 < obj.y or charac.y1 > obj.y):
collision
else:
no collision
Circle Circle
To have a circle-circle collision, there is a collision if the distance between the two centers is smaller than the sum of the rfadii. To compute the distance between two points, use Pythagore.
distance = pythagore(center1X - center2X, center1Y - center2Y) # = sqrt(a*a + b*b) = sqrt(a**2 + b**2)
if distance < radius1 + radius2:
collision
else:
no collision

Let's notice that the condition distance < rayon1 + rayon2 is equivalent to distance² < (rayon1 + rayon2)², therefore the computation can be done with no square root:
dx = circle1x - circle2x
dy = circle1y - circle2y
if dx ** 2 + dy ** 2 < (radius1 + radius2) ** 2:
collision
else:
no collision
Point Circle
To have a point-circle collision, we can see the point as a zero-radius circle.
dx = circlex - px
dy = circley - py
if dx ** 2 + dy ** 2 < radius ** 2:
collision
else:
no collision
Circle Rectangle
Here is the code:
# cx,cy = circle's center
# rx,ry = rectangle's center
# w,h = rectangle's width/height
hrx, hry = w/2, h/2
clampX = min(max(cx - rx, -hrx), +hrx)
clampY = min(max(cy - ry, -hry), +hry)
closestX = rx + clampX
closestY = ry + clampY
if pythagore((closestX, closestY), (cx,cy)) <= radius:
collision
else:
no collision
This code comes from this page, chapter AABB - Circle collision detection.
Let's notice that doing
y = min(max(x, m), M)
is equivalent to:
y = x
if y < m: # not bigger than the minimum!
y = m
else:
if y > M: # not smaller than the maximum!
y = M
The site learnopengl.com is a very good tutorial to learn modern (2010) opengl, this includes shaders programming.
Bounce
When a ball (or a light ray) bounces on a wall, this is what happens:
Angle
One way to see the bounce is that the angle changes:
- When the ball bounces on the right (or left) wall, we then have θ' = 180° − θ.
- When the ball bounces on the bottom (or top) wall, we then have θ' = − θ.
One can also find the formula for any wall angle α. For the right wall, we then have α = 270°.
Vector
One can also see that with vectors, we try to compute the new velocity vector v'.
- For the left (or right) wall, we then have x' = − x and y' = y.
- For the top (or bottom) wall, we then have y' = − y and x' = x.
General case
In the general case, that also works in 3D, is when the wall has a normal vector n, the formula used is the reflexion law:
n = n / norm(n) # we normalize n, norm(n) = sqrt(n.x ** 2 + n.y ** 2)
new_v = v + 2 * dot(n, v) * n # dot is the dot product, dot(n,v) = n.x * v.x + n.y * v.y
Let's notce that the sign of the dot product appearing in the formula gives us the information does the ball go in the wall scalaire présent permet de savoir si la balle rentre dans le mur (negative product) or not (positive), if the product is zero, then it moves paralaly to the wall (v and n are perpendicular).
In 3D, the bounce is on a plane, places also have normals.
Display integers
To display informations like the number of lifes or the current score, we have two choices:
- Either using numbers. See Voir pygame8_texte.py et theorie2 (to know more).
- Either display one star for each point won / life left. This will make you work on the loops!
Delete correctly from a list
Often in games, one needs to delete from a list some elements that have a property.
For example, one wants to delete all the coins that are in collision with the player, or one would like to remove from the list of players the ones that have no hp left.
Let's take an easier example, we have a list of integers and we want to delete all the numbers that are greater than 5.
Naive approach does not work:
L = [1,2,7,8,1,3,6,7]
i = 0
while i < len(L):
if L[i] > 5:
del L[i]
i = i + 1
The loop will jump one element. I invite you to test the code on pythontutor to see the problem.
The solution is to not incremet the counter when the element is deleted:
L = [1,2,7,8,1,3,6,7]
i = 0
while i < len(L):
if L[i] > 5:
del L[i]
else:
i = i + 1
Another tip: create a variable to remember you want to delete the element.
L = [1,2,7,8,1,3,6,7]
i = 0
while i < len(L):
to_delete = False
if L[i] > 5:
to_delete = True
if to_delete:
del L[i]
else:
i = i + 1
Another tip a little less efficient but probably easier to code: create a garbage list:
L = [1,2,7,8,1,3,6,7]
garbage = []
for x in L:
if i > 5:
garbage.append(x)
for y in garbage:
L.remove(y)
Infinite world
This technique is Useful to have a world much larger that the size of the window.
Imagine a game with a character (image), some coins (circles), some ennemies (circles) and some buildings (rectangles), each has their respective class, their position (x,y), width (w), height (h), radius (r) and are all in their respective list.
My windows size is (700, 500) but my world is much larger.
The classical approach is to draw the scene like this:
# character
image_charac.blit(screen, [charac.x, charac.y])
# scene
for c in coin_list:
pygame.draw.circle(screen, YELLOW, [c.x, c.y], c.r)
for e in ennemy_list:
pygame.draw.circle(screen, RED, [e.x, e.y], e.r)
for b in building_list:
pygame.draw.rect(screen, BLUE, [b.x, b.y, b.w, b.h])
I could only see the points between (0,0) and (700,500) of my world.
The idea is to have a caméra that moves, here it is in (0,0) but if it was in (50,100), we would see the points from (50,100) to (750,800).
An element with world position is (150,270) would be seen drawn on screen at (100,170).
We must then draw all our elements at (x - camera.x, y - camera.y).
# character
image_charac.blit(screen, [charac.x - camera.x, charac.y - camera.x])
# scene
for c in coin_list:
pygame.draw.circle(screen, YELLOW, [c.x - camera.x, c.y - camera.x], c.r)
for e in ennemy_list:
pygame.draw.circle(screen, RED, [e.x - camera.x, e.y - camera.x], e.r)
for b in building_list:
pygame.draw.rect(screen, BLUE, [b.x - camera.x, b.y - camera.x, b.w, b.h])
For a rpg, the simplest is generally to code that at each tick, the camera is on the player. We will add the following logic at each tick:
# the camera is following the character
camera.x = charac.x
camera.y = charac.y
Because the character is drawn in (charac.x - camera.x, charac.y - camera.y), the character will always be drawn at (0,0), we can put the camera a bit further such that the character is always at the center of the screen (350,250):
# the camera is following the character
camera.x = charac.x - 350
camera.y = charac.y - 250
The on screen position will then be (charac.x - camera.x, charac.y - camera.y) = (charac.x - (charac.x - 350), charac.y - (charac.y - 250)) = (+350, +250)
But you can also choose a more fantaisist camera! For a game I created, I applied the spring equations with linear friction between the camera and the player and the result was awesome!
# the camera is following the character but with a small delay
alpha = 0.80 # 80% of the displacement is token at each tick
camera.x = camera.x + alpha * (charac.x - 350 - camera.x)
camera.y = camera.y + alpha * (charac.y - 250 - camera.y)
 Français ici !
Français ici !