Mathematics: Trigonometry, vectors and matrices
Presentation exercises
Here are some math exercises very handy for 2D videogames, the theory is in the sections below, exercise number 1 use the Pythagorean theorem, exercises number 2 and 3 use trigonometry, exercise number 4 use the vector concept.
Exercise 2: Go forward
Exercise 3: Look at
Exercise 4: Unit vector
Pythagoras
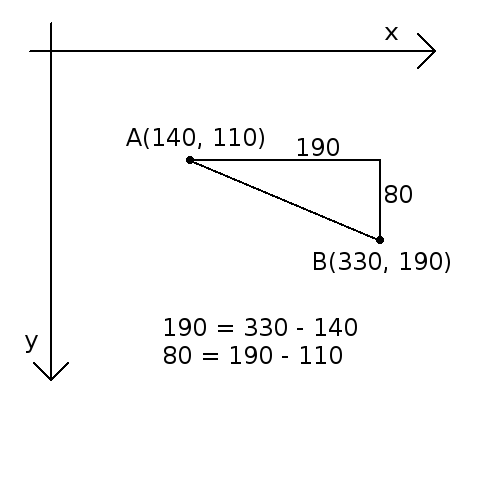
- What is the length of the diagonal of a square of side 1cm?
- If I have a right triangle (a triangle where one of its angle is 90 degrees) that has a side of length 5cm, and another of length 2cm, what will be the length of the last side length?
Draw on a piece of paper those two examples and measure the length that are asked, did you know that there exist a formula that solve those problems?
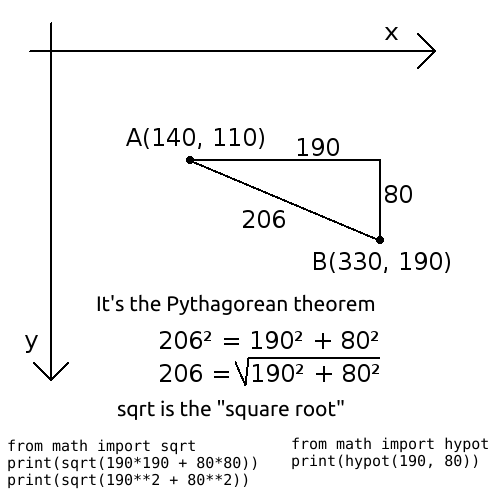
Those two questions can be answered using the Pythagorean theorem, for example $\sqrt{2} \approx 1.41 \text{cm}$ is the answer to the first question.
Remember that the square root of a number $x$ is the number that when multiplied by itself gives $x$. Therefore, $\sqrt{9} = 3$ because $3 \times 3 = 9$, or by using exponents, $3^2 = 9$. The square root of 2 is a number with an infinite number of digits after the decimal point! It's called an irrationnal number. More infos on irrationnal numbers can be found online.
$\sqrt{2} \approx 1.41$ is indeed the square root of 2 because $\sqrt{2} \times \sqrt{2} = 2$, indeed, $1.41 \times 1.41 = 1.9880 \approx 2$.
A calculator is capable to do square roots, python can do it via math.sqrt(2) when you wrote import math at the beginning of the file.
math is a python module, more info on modules
here.
You can easily find informations on the Pythagoreas theorem all over the internet by writing on Google Pythagorean theorem. Or by simply going on Wikipedia or on mathisfun.
For more informations, look at the Pythagoras theorem on Clipedia (french only at the moment).
Do not hesitate to put the video in fullscreen, to stop or go back if you want to, or even to look at the video in fast-forward by clicking on the speed button of the player. Click on linked videos at the bottom of the video to look at other videos of the same subject.
Trigonometry
Trigonometry makes it possible to link angles and distances, thanks to the basic notions, one can answser to questions such as:
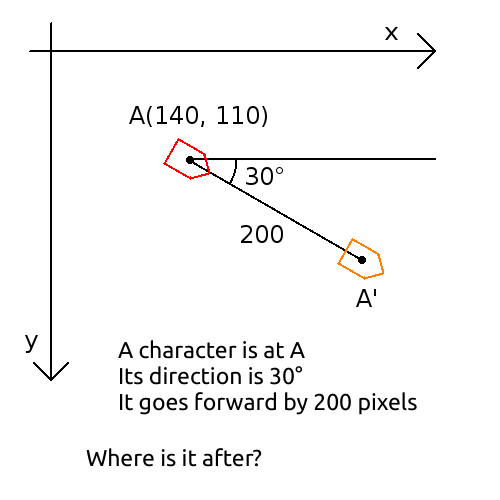
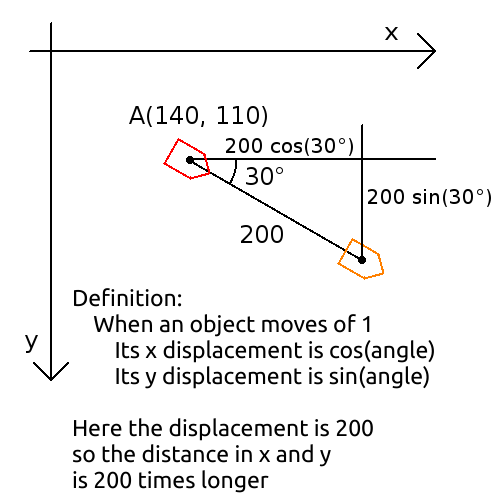
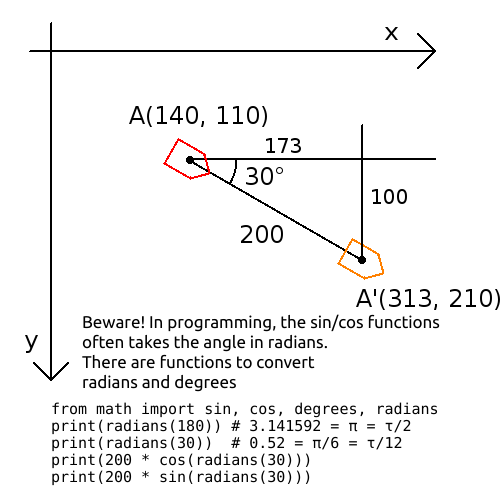
- In 2D, a character is on the point A of coordinates (x = 140, y = 100) meters, it is looking at 30° and go forward 200 meters, where is it now?
- A triangle has one side of length 1, one other side of length 2, separated by an angle of 30°, what are the lengths of the other sides and what are the values of the other angles?
- What is the height of a triangle of sides 1, 2 and 3?
- How to perfectly cut a pizza in 6?
In spoken language, we'll prefer to say the short version trig.
Cosine and sine
The basics of trigonometry is the definition of the sine of an angle and the cosine of an angle.
A point P at distance 1 of the origin that has an angle $\theta$ with x axis (in the direction of y axis) has the coordinates $(x = \cos\theta,\ y = \sin\theta)$:
By definition, using a lot of words, one have the cosine of an angle is the coordinate x of the point at distance 1 placed at that angle with respect to x axis and the sine of an angle is the coordinate y of the point at distance 1 placed at that angle with respect to x axis.
On my drawing, the angle is equal to 34° and the point has approximately the coordinates $(0.82, 0.55)$ (I measured!), one has $\cos(34°) = 0.82$ and $\sin(34°) = 0.55$
Click on the previous figure to see the numerical values.
Par la définition, vous pouvez déja répondre à ces questions :
- Quelles sont les longueurs et les angles d'un triangle rectangle dont un angle de 34° dont le plus grand côté (l'hypothénuse) est de longueur 1 ?
- Comment nommeriez vous les deux autres côtés ? On les appelle généralement côté adjacent à l'angle et opposé à l'angle, qui ici vaut 34°.
- Même question mais l'hypothénuse est de longueur 5.
- Même question mais l'hypothénuse est de longueur r.
- Même question mais l'angle vaut $\theta$
Ou aux questions, est-ce qu'il existe un angle...
- ...dont le cosinus est plus grand que 1 ?
- ...dont le cosinus vaut zéro ?
- ...dont le sinus vaut 0.82 ? Quel est le rapport entre cet angle et 34 degrés ?
- ...dont le cosinus est négatif ? Réponse un peu plus bas !
Une autre manière bien commode de voir le sinus (et le cosinus) est via le sinus comme mouvement de rotation sur Clipedia.
Conventions d'axe Y
Beware, if the y axis is to the bottom (as it is often in computer sciene), the angle rotates in the other direction!
- When Y is in the top direction, clockwise is the direction where the values of the angle go down whereas anti-clockwise is the direction where the values go up.
- When Y is in the bottom direction, clockwise is the direction where the values of the angle go up whereas anti-clockwise is the direction where the values go down.
Because of the two different Y-axis convention, I prefer not to talk about trigonometric direction of rotation, or I like to say that the trigonometric direction of rotation is the direction that is such as cos(1°) and sin(1°) are positives.
Calculators and computers
In the old times, we had no calculators, then we read tables... Now we do and we have have computers ! Here, my example in Python:
>>> from math import cos, sin, radians, degrees
>>> cos(radians(34))
0.82
>>> sin(radians(34))
0.55
We'll see later why we must write radians, but for now just know that radiands are a more mathematical unit for angles so must natrally convert degrees to radians.
Le code précédent peut se simplifier en téléchargeant mon fichier vecutils :
>>> from vecutils import cosd, sind
>>> cosd(34)
0.82
>>> sind(34)
0.55
Vous pouvez également regarder le fichier vecutils pour voir la définition de la fonction cosd et sind, rien de bien sorcier.
from math import radians, degrees, sin, cos
def sind(x):
return sin(radians(x))
def cosd(x):
return cos(radians(x))
On a calculator, there is a button to switch the execution mode of cos and sin.
Utiliser Python comme calculette est aussi facile qu'utiliser une calculette, sauf qu'on peut faire beaucoup plus, je suis en train d'écrire un petit tutoriel sur Python comme calculette (il sera sur cette page).
Distance r
Now, if the point is at distance 2 and not 1, everything is 2 times bigger, its coordinates are therefore $(x = 2\cos\theta,\ y = 2\sin\theta)$. In more general terms, if its distance is $r$, its coordinate will then be $(x = r\cos\theta,\ y = r\sin\theta)$.
Quand vous avez un triangle rectangle, imaginez d'abord que qu'il est unitaire (l'hypothénuse de longueur 1), puis finalement multipliez tout par la vraie longueur de l'hypothénuse.
Negative coordinates
If the angle is between 90° et 270°, the x coordinate is then negative. If the angle is between 180° and 360°, the y coordinate will be negative. One can see that the sine and the cosine of an angle can be negative!
The circle that you can see on the drawing is often called the trigonometry circle, because it shows the basic concepts of trigonometry, however, because the the circle has a radius 1, the cosine and the sine of an angle are always between −1 and 1.
The sine cosine relation
By applying pythagoras in the right-angled triangle on the image, one has:
$(\sin\theta)^2 + (\cos\theta)^2 = 1^2$ $\iff \sin^2\theta + \cos^2\theta = 1$
And that's true for every angle $\theta$, admirable isn't it ?
Small and big angles
An angle can be negative, an angle of −45° corresponds to an angle of 315°, indeed, rotate 45° to the left is the same as rotate 315° to the right, more generally, an angle of −x degrees corresponds to an angle of 360−x degrees.
An angle may be bigger than 360 degrees, indeed, rotating 45° is the same as rotating 405° (45° plus one turn of 360°), more generally, an angle of x degrees corresponds to an angle of 360+x degrees.
One can do more than one turn, an angle of 45° is equivalent to an angle of 45°+360°+360°+360°...
The point corresponding to angle −45° will then have the same coordinates than the angle 315° and the point corresponding to angle 45° will then have the same coordinates than the angle 405°.
One has then: $ \begin{cases} \cos(360° - \theta) = \cos(-\theta) \\ \sin(360° - \theta) = \sin(-\theta) \end{cases} $ and $ \begin{cases} \cos(\theta + 360°) = \cos \theta \\ \sin(\theta + 360°) = \sin \theta \end{cases} $
Le cosinus est très sympa pour beaucoup de propriétés, comme par exemple
$\cos(-\theta) = \cos\theta$
Alors que le sinus introduit un signe − :
$\sin(-\theta) = -\sin\theta$
On voit de manière évidente les propriétés énoncées.
Tangent
By definition: $\tan\theta = \cfrac{\sin\theta}{\cos\theta}$ the tangent of angle $\theta$, also written $\tan\theta$. The tangent is defined by the ratio of sine over cosine.
The tangent can also be seen as a coordinate on the trigonometric circle:
The tangent is equal to the y coordinate of the intersection of the straight line $x = 1$ and the straight line $OP$. It's easy to prove that the tangent is the ratio of the sinus and cosinus, one can see to similar triangles.
Quand vous avez un triangle rectangle et vous vous intéressez aux deux petits côtés, imaginez d'abord que le côté adjacent à l'angle vaut 1, puis multipliez par la vraie longueur du côté.
Il y a aussi la cotangente définie comme $\cfrac{\cos\theta}{\sin\theta}$ $= \cfrac{1}{\tan\theta}$ ou comme l'intersection de la droite $y = 1$ et de la droite $OP$ mais elle est rarement utilisée.
When the angle is between 90 and 180 degrees (second quadrant), the sine is positive and the cosine is negative, therefore the tangent is negatif. On the drawing, one can see that the intersection between the two straight lines is beneath the x axis.
When the angle is 90°, the sine is 1, the cosine is 0 and the tangent does not exist, or is equal to $\frac{1}{0} = +\infty$. When the angle is equal to −90°, the sine is equal to −1, the cosine is 0, then the tangent is equal to $\frac{-1}{0} = -\infty$, the cotangent has the same considerations for angles 0 and 180 degrees.
Right angled triangle
In a circle of radius $r$ with an angle $\theta$, one can observe a right-angled triangle.
In a right angled triangle, the opposite side of the right angle is called the hypothenuse (length h). When one talks about one of the two angle, one will talk about the adjacent side (length a) and the opposite side (length o).
One can conclude that, in every right-angled triangle, the sine, cosine and tangent of the angles represent ratios, a division of two length:
$\begin{cases} r\ \sin\theta = o \\ h = r \\ \end{cases} \iff$ $\sin\theta = \cfrac{o}{h}$
$\begin{cases} r\ \cos\theta = a \\ h = r \\ \end{cases} \iff$ $\cos\theta = \cfrac{a}{h}$
$\tan\theta$ $= \cfrac{\sin\theta}{\cos\theta}$ $= \cfrac{ \frac{o}{h} }{ \frac{a}{h} }$ $= \cfrac{o}{a}$
- The sine of an angle is equal to the length of the side opposite to the angle divided by the length of the hypothenuse: $\sin\theta = \frac{o}{h}$
- The cosine of an angle is equal to the length of the side adjacent to the angle divided by the length of the hypothenuse: $\cos\theta = \frac{a}{h}$
- The tangent of an angle is equal to the length of the side opposite to the angle divided by the length of the side adjacent: $\tan\theta = \frac{o}{a}$
A well known mnemonic is SOHCAHTOA, the Sine of the angle is equal to the length of the Opposite side divided by the length of the Hypothenuse, the Cosine of the angle is equal to the length of the Adjacent side divided by the length of the Hypothenuse, the Tangent of the angle is equal to the length of the Opposite side divided by the length of the Adjacent.
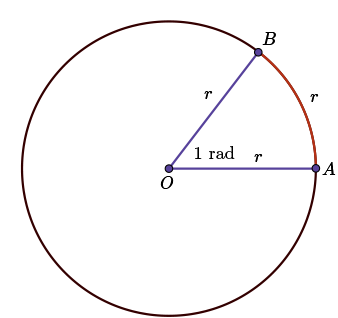
The radian
The radian is an angle unit more mathematical, such that 360 degrees is $2\pi$ radians becase $2\pi$ is the circumference of a circle of radius 1.
At angle 1 radian, one has the length of the arc (in red) is equal to the radius of the circle (in blue):
Some mathematicians do not like $\pi$, and prefer to use $\tau = 2\pi$. We then have $\tau = 2\pi = 6.283185...$
therefore, 360 degrees, it's a full turn, it's $\tau$ radians! Talking about $\tau$ radians is like talking about turns, therefore $\frac{3}{4}\tau$ radians is the angle that does $\frac{3}{4}$ of one turn, then $\frac{3}{4}360 = 270$ degrees.
To convert from degrees to radians:
$360\ \text{deg} = \tau\ \text{rad}$ $\iff x\ 360\ \text{deg} = x\ \tau\ \text{rad}$ $\iff x\ \text{deg} = x \frac{\tau}{360}\ \text{rad}$ $\iff x\ \text{deg} = (x \times \tau / 360)\ \text{rad}$ $= (x \times \pi / 180)\ \text{rad}$
And from radians to degrees:
$x\ \text{deg} = (x \times \tau / 360)\ \text{rad}$ $\iff x\ \text{rad} = (x \times 360 / \tau)\ \text{deg}$ $= (x \times 180 / \pi)\ \text{rad}$
Let's recall that $\tau = 2\pi = 6.283185...$ then $1\ \text{rad} \approx 57°$.
from math import tau
>>> tau # since Python 3.6
6.2831
Python nous permet de convertir du degré au radian :
from math import radians, degrees
>>> radians(360)
6.2831
>>> degrees(1)
57.29
Attention, les fonctions cos et sin attendent des radians !
>>> from math import cos, sin
>>> cos(radians(34))
0.82
Un petit mot sur le cosinus
Le sinus a en fait été découvert en premier, vous pouvez voir l'histoire sur wikipedia, ensuite le cosinus était défini par le sinus de l'angle complémentaire du sinus. On a donc :
$\sin(90° - \theta) = \cos\theta$
Et vu que le complémentaire du complémentaire d'un angle c'est cet angle, on a aussi :
$\cos(90° - \theta) = \sin\theta$
Ou encore en radians (sacré pidemi) :
$\cases{ \sin(\tfrac{\pi}{2} - \theta) = \cos\theta\\ \cos(\tfrac{\pi}{2} - \theta) = \sin\theta }$
Ou en tauiste (on parle bien d'un quart de tour non ? Sacré tauquart) :
$\cases{
\sin(\tfrac{\tau}{4} - \theta) = \cos\theta\\
\cos(\tfrac{\tau}{4} - \theta) = \sin\theta
}$
Formule d'addition
On a vu beaucoup de cas spéciaux, mais une formule $\cos(a + b)$ existe aussi.
On se rappellera de la forme symmétrique de $\cos(a - b)$ :
- $\cos(a - b) = \cos a \cos b + \sin a \sin b$
Et il est ensuite facile de démontrer les 4 autres formules :
- $\cos(a + b) $ $= \cos(a - (-b))$ $\cos a \cos(-b) + \sin a \sin(-b)$ $= \cos a \cos b - \sin a \sin b$
- $\sin(a + b)$ $ =\cos(90° - (a + b))$ $ =\cos(90° - a - b)$ $ =\cos((90° - a) - b)$ $ =\cos(90° - a) \cos b + \sin(90° - a) \sin b$ $ =\sin a \cos b + \cos a \sin b$
- $\sin(a - b) $ $= \cos a \cos b + \sin a \sin b$
La première formule est facile à mémoriser et se démontre le plus facilement avec le produit scalaire (
$\vec{1}_a \cdot \vec{1}_b = \cos\theta$ où $\theta$ est l'angle entre les deux,
donc angle de l'un moins l'angle de l'autre, donc $\theta = \theta_a - \theta_b$,
donc $\vec{1}_a \cdot \vec{1}_b = \cos(a - b)$
or, on sait que $\vec{1}_r = (\cos \theta_r,\ \sin\theta_r)$
on a donc $(\cos \theta_a,\ \sin\theta_a) \cdot (\cos \theta_b,\ \sin\theta_b) = \cos(\theta_a - \theta_b)$
donc $\cos(\theta_a - \theta_b) = \cos\theta_a \cos\theta_b + \sin\theta_a \sin\theta_b$ CQFD
)
ou par géométrie (voir loi d'addition des sinus et cosinus sur clipedia).
Cette formule marche donc pour tous les cas particuliers intuitifs dont on avait parlé :
- $\text{sincos}(360°+\theta)$
- $\text{sincos}(360°-\theta)$
- $\text{sincos}(-\theta)$ $=\text{sincos}(0 - \theta)$
- $\text{sincos}(90°-\theta)$
Trouver l'angle, les fonctions d'Arc
[Section en construction]Clipedia
More infos on trigonometry and the radian on clipedia! (french only at the moment)
Do not hesitate to put the video in fullscreen, to stop or go back if you want to, or even to look at the video in fast-forward by clicking on the speed button of the player. Click on linked videos at the bottom of the video to look at other videos of the same subject.
Vectors
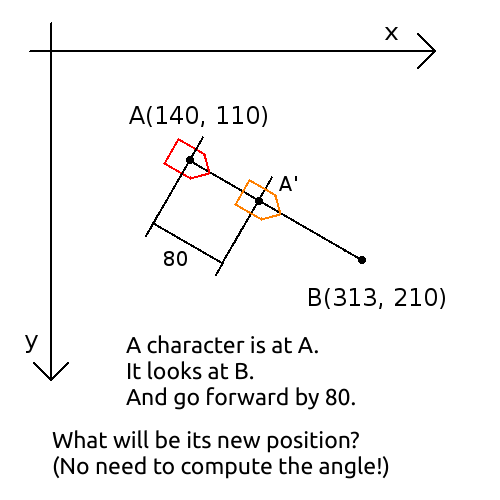
Exercise 4 uses a concept called vector. In one word, a vector is a displacement. Vectors permit to do some operations the same way in 1D, 2D and 3D. The concept of displacement is indeed common to the 3 dimensions.
For an other explanation, more detailed, on vectors, I suggest these 3 videos [1] [2] [3] on the subject on Clipedia (french only at the moment). Do not hesitate to put the video in fullscreen, to stop or go back if you want to, or even to look at the video in fast-forward by clicking on the speed button of the player. Click on linked videos at the bottom of the video to look at other videos of the same subject.
Or this video on vectors part of the playlist about linear algebra from channel 3Blue1Brown.
Basic operations

Imaginez que vous êtes sur un échiquier en case b1 et que vous vous déplacez en case c3, vous faites un déplacement de 1 case vers la droite et 2 cases vers le haut. Si on appelle votre vecteur de déplacement $\vec{d}$, on notera $\vec{d} = (1,\ 2)$. Les nombres 1 et 2 sont appelés les composantes du vecteur $\vec{d}$.
Quand on parle de vecteur, les nombres sont souvent appelés scalaires, on dira donc les vecteurs et les scalaires ou les composantes d'un vecteur sont des scalaires.
La flèche au dessus de la lettre d permet de rappeler que $\vec{d}$ est un vecteur. D'autres notations existent : sans la pointe de la flèche $\bar{d}$, en majuscule $D$, ou sur ordinateur, en gras $\mathbf{D}$.
Géométriquement, la flèche peut se déplacer, le déplacement de b1 vers c3 est le même que celui de g1 à h3.
Un déplacement peut avoir des composantes négatives, si je suis en b8 et que je vais en c6, $\vec{d} = (1,-2)$. Se déplacer de 2 cases vers le bas, c'est la même chose que de se déplacer de −2 cases vers le haut.
Il existe 3 opérations de base sur les vecteurs 2D : l'addition, la multiplication par un nombre et la norme.
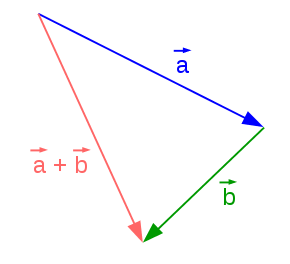
Addition
$\vec{v} + \vec{w} = (v_x + w_x,\ v_y + w_y)$
Exemple: $(3,\ 5) + (-2,\ 1) = (1,\ 6)$.
Un déplacement de 3 cases vers la droite et 5 cases vers le haut + Un déplacement de −2 cases vers la droite et 1 case vers le haut = Un déplacement de 1 case vers la droite et 6 cases vers le haut.
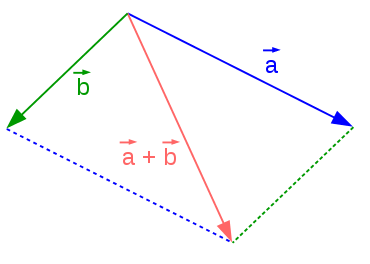
Voici une représentation géométrique de l'addition vectorielle.
Multiplication par un nombre (un scalaire)
$k \cdot \vec{v} = (k \cdot v_x,\ k \cdot v_y)$
Exemple: $2 \cdot (-4,\ 3) = (-8,\ 6)$
2 fois Un déplacement de −4 cases vers la droite et 3 cases vers le haut = Un déplacement de −8 cases vers la droite et 6 cases vers le haut.
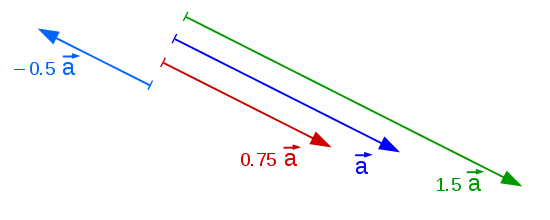
Voici une représentation géométrique de la multiplication par un nombre.
Norme (ou longueur, taille)
$\|\vec{v}\| = \sqrt{v_x^2 + v_y^2}$
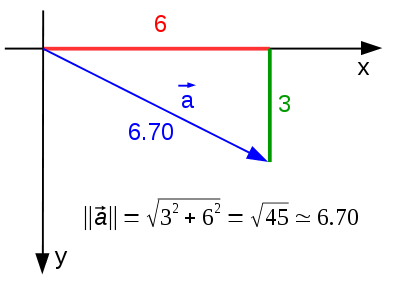
$\|(6,3)\| = \sqrt{6^2 + 3^2}$ $= \sqrt{45}$ $\simeq 6.70 $
La norme est calculée avec pythagore. Voici une représentation graphique du calcul de la norme de $\vec{a} = (6, 3)$
Remarquez que cela marche également avec des composantes négatives !
$\|(-6,3)\| = \sqrt{(-6)^2 + 3^2}$ $= \sqrt{6^2 + 3^2}$ $= \sqrt{45}$ $\simeq 6.70 $
Deux vecteurs particuliers forment la base pour tous les vecteurs, c'est $\vec{e}_x = (1,0)$ et $\vec{e}_y = (0,1)$. Ainsi tout vecteur $\vec{v} = (a,b)$ peut s'écrire $\vec{v} = a \cdot \vec{e}_x + b \cdot \vec{e}_y$.


D'autres notations existent pour les vecteurs de base, on retrouve $\vec{e}_1$, $\vec{e}_2$ ou encore $\vec{i}$, $\vec{j}$ ou $\mathbf{i}$, $\mathbf{j}$ ou vu qu'ils sont de norme 1, $\vec{1}_x$, $\vec{1}_y$ ou $\mathbf{\hat{i}}$, $\mathbf{\hat{j}}$ ou sans le point $\hat{\imath}$, $\hat{\jmath}$, ils sont fous ces humains.
- $\vec{a} = (6,\ 3) $ $= 6\, \vec{e}_x + 3\, \vec{e}_y $ $= 6\, \vec{e}_1 + 3\, \vec{e}_2$
- $\mathbf{a} = (6,\ 3) $ $= 6 \mathbf{i} + 3 \mathbf{j} $ $= 6 \mathbf{\hat{i}} + 3 \mathbf{\hat{j}}$ $= 6 \hat{\imath} + 3 \hat{\jmath}$
Opérations déduites
Depuis ces 3 opérations de base, nous déduisons le reste, remarquez que généralement on introduit les vecteurs avec le concept que j'appelle ici soustraction.
Vecteur opposé
$- \vec{v} = (-1) \cdot \vec{v} = (-v_x,\ -v_y)$
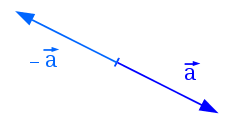
On dit que ce vecteur a la même direction, mais un sens opposé.
La somme de ces deux vecteurs donne bien le vecteur nul : $\vec{v} + (-\vec{v}) = \vec{0} = (0,0)$
Soustraction
$\vec{v} - \vec{w} = \vec{v} + (- \vec{w}) = (v_x - w_x,\ v_y - w_y)$
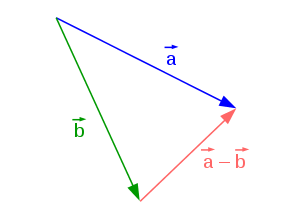
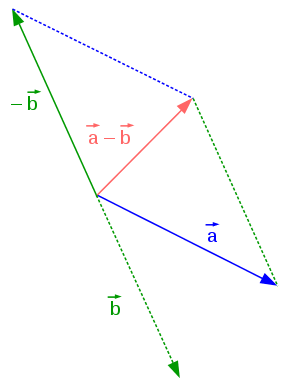
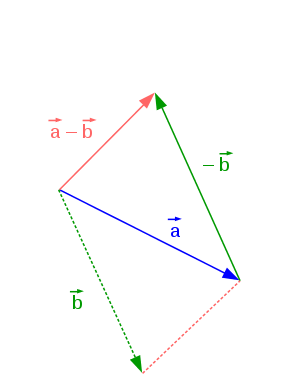
Le meilleur moyen de voir la soustraction est de poser la question quel est le déplacement $\vec{d}$ qui va du point $\vec{a}$ au point $\vec{b}$ ? $\vec{d} = \vec{b} - \vec{a}$. Attention, j'ai bien dit $\vec{b} - \vec{a}$ et pas $\vec{a} - \vec{b}$, pour savoir le déplacement, on fait la position finale moins la position initiale.
On notera $\vec{AB}$ le vecteur qui va du point A au point B, on a $\vec{AB} = \vec{b} - \vec{a}$.
Quand on a trois points $A$, $B$, $C$, on a naturellement : $\vec{AB} + \vec{BC} = \vec{AC}$,
c'est la relation de Chasles,
elle est évidente quand on voit ça comme une soustraction
(
$\vec{AB} + \vec{BC}$
$= (\vec{b} - \vec{a}) + (\vec{c} - \vec{b})$
$= \vec{b} - \vec{a} + \vec{c} - \vec{b}$
$= - \vec{a} + \vec{c}$
$= \vec{c} - \vec{a}$
$= \vec{AC}$
)
ou via un dessin.
Et si on inverse les deux points, on obtient le vecteur opposé : $\vec{BA} = - \vec{AB}$, encore une fois, évident ($\vec{AB} + \vec{BC} = \vec{AC}$).
Division par un nombre (un scalaire)
$\vec{v} / k = (1/k) \cdot \vec{v}$

Vecteur normalisé: le vecteur de taille 1 (ou vecteur unitaire)
$\vec{1}_v = \vec{v} / \|\vec{v}\|$
Si je multiple un vecteur par 2, sa norme (taille) est également multipliée par 2. De même, si un vecteur de longueur 5 est divisé par 5, il devient de longueur 1. Le vecteur normalisé $\vec{1}_v$ est donc le vecteur dans la même direction et sens que $\vec{v}$, mais de longueur $1$. Un exemple ici :
Si $\vec{d} = (4,3)$ alors $\vec{1}_d$ $= \vec{d}/\|\vec{d}\|$ $= (4,\ 3)/5$ $= (0.80,\ 0.60)$
$\vec{d} = (4,3)$ $\implies \vec{1}_d$ $= \vec{d}/\|\vec{d}\|$ $= (4,\ 3)/5$ $= (0.80,\ 0.60)$
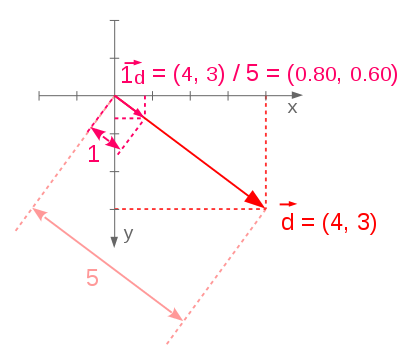
Un avantage pratique d'un vecteur normalisé, est que si je le multiple par 5, il sera de taille 5 !
Dans la littérature anglaise on retrouve la notation $\hat{v}$ ou $\mathbf{\hat{v}}$ pour $\vec{1}_v$, l'accent circonflexe signifiant que la norme vaut 1.
Exemple
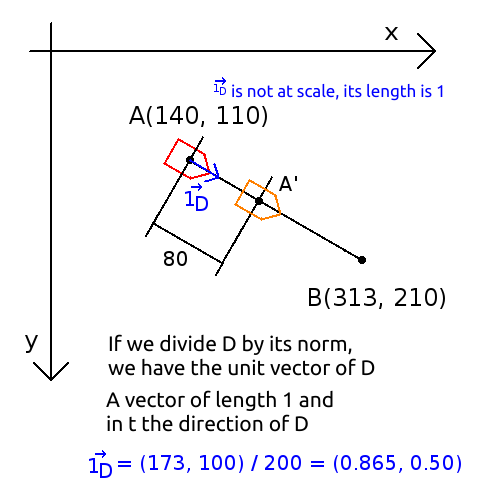
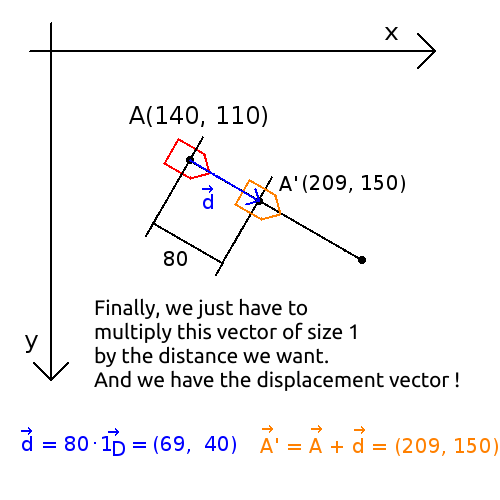
Je vais du point $A(6,3)$ (mètres) au point $B(4,7)$ (mètres), j'ai parcouru une distance de $4.47m$.

Pour ce déplacement, je peux dire :
- Je me suis déplacé de −2 mètres en x et +4 mètres en y
- Je me suis déplacé de 4.47m à 116.5°
Une direction peut être représentée par un angle ($\theta$) ou un vecteur unitaire, un vecteur unitaire a une norme = $1$. L'utilité d'un tel vecteur est que si on le multiplie par un nombre positif $n$, le vecteur final aura la norme $n$.
-
On peut représenter le déplacement via ses composantes x,y :
$\vec{d} = \vec{AB}$ $= \vec{b} - \vec{a}$ $= (4,\ 7) - (6,\ 3)$ $= (-2,\ 4)$
-
Ou avec la direction et la norme :
Vecteur unitaire depuis l'angle
$\vec{1}_d = (\cos\theta,\ \sin\theta) $$= (\cos 116.5°,\ \sin 116.5°)$ $= (-0.44,\ 0.89)$
Vecteur unitaire depuis un vecteur
$\vec{1}_d $$= \vec{d} / \|\vec{d}\| = (-2,\ 4) / 4.47$ $= (-0.44,\ 0.89)$
Vecteur depuis un vecteur unitaire et une longueur
$\vec{d} $$= \|\vec{d}\| \cdot \vec{1}_d$ $= 4.47 \cdot (-0.44,\ 0.89)$ $= (-2,\ 4)$
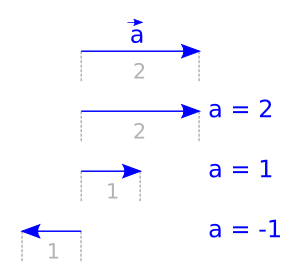
Une dernière petite notation souvent rencontrée, quand on a un vecteur $\vec{a}$, on note souvent $a$ (sans flèche) pour la norme signée. $a$ peut donc être négatif (dans ce cas le vecteur est renversé).
Ou encore, on dira que $a$ est la projection de $\vec{a}$ sur la droite dirigée définie par le vecteur $\vec{a}$.
Voilà, j'espère que tu as mieux compris l'exercice 4 et que tu n'as pas peur d'utiliser les vecteurs en physique ou dans des opérations plus complexes dans la section suivante !
Résumé
- Un vecteur $\vec{v} = (v_x,v_y)$, c'est un déplacement, avec ses composantes $v_x,v_y$.
- $\vec{v} + \vec{w} = (v_x + w_x,\ v_y + w_y)$
- $k \cdot \vec{v} = (k \cdot v_x,\ k \cdot v_y)$
- $\|\vec{v}\| = \sqrt{v_x^2 + v_y^2}$
- $- \vec{v} = (-1) \cdot \vec{v}$ $= (-v_x,\ -v_y)$
- $\vec{v} - \vec{w} = \vec{v} + (- \vec{w})$ $= (v_x - w_x,\ v_y - w_y)$
- $\vec{1}_v = \vec{v} / \|\vec{v}\|$
- $\|\vec{1}_v\| = 1$
- $\vec{1}_v = (\cos\theta,\ \sin\theta)$
- $\|k \vec{1}_v\| = |k|$
Opérations vectorielles
Voici une vue d'ensemble d'autres opérations vectorielles utiles dans d'autres contextes.
Équation de droite
Une droite (2D ou 3D !) est représentée avec un point $\vec{p}$ et un déplacement $\vec{d}$. On a : $\vec{r}(t) = \vec{p} + t \cdot \vec{d}$ où $t$ est un nombre réel.
Le déplacement $\vec{d}$ est appelé un vecteur directeur de la droite, si l'on connaît deux points de la droite $\vec{p}_0$ et $\vec{p}_1$, il est facile de calculer un vecteur directeur $\vec{d} = \vec{p}_1 - \vec{p}_0$.
Pour toute valeur de $t$, on obtient un point. Par exemple, la droite passant par $\vec{p} = (1,2)$ de vecteur directeur $\vec{d} = (2,-3)$ contient ces 5 points :
| $\vec{r}(0) $ | $= (1,2) + 0 \cdot (2,-3) $ | $= (1,2)$ |
| $\vec{r}(0.5) $ | $= (1,2) + 0.5 \cdot (2,-3) $ | $= (1.5,-0.5)$ |
| $\vec{r}(1) $ | $= (1,2) + 1 \cdot (2,-3) $ | $= (3,-1)$ |
| $\vec{r}(2) $ | $= (1,2) + 2 \cdot (2,-3) $ | $= (5,-4)$ |
| $\vec{r}(-1) $ | $= (1,2) + (-1) \cdot (2,-3) $ | $= (-1,5)$ |
Si $t$ est négatif, le point de l'autre côté du vecteur $\vec{d}$, comme par exemple le point $\vec{r}(-1)$ sur la figure précédente.
Si $\vec{d}$ est normé, le vecteur $\vec{r}(t)$ sera toujours à distance $|t|$ de $\vec{p}$, on peut donc facile résoudre le problème suivant : quels sont les deux points de la droite à distance $k$ de $\vec{p}$ ? Il s'agit de $\vec{p} \pm k\ \vec{1}_d$
Pour représenter un segment, il suffit de prendre $t \in [0,1]$
Plus d'infos sur Clipédia.
Produit scalaire
Une opération pratique est le produit scalaire noté $\vec{a} \cdot \vec{b}$ ou parfois $\langle \vec{a}, \vec{b} \rangle$, c'est une opération qui prend deux vecteurs et renvoie un nombre (un scalaire).
Une des propriétés de ce produit est que deux vecteurs perpendiculaires ont un produit scalaire nul.
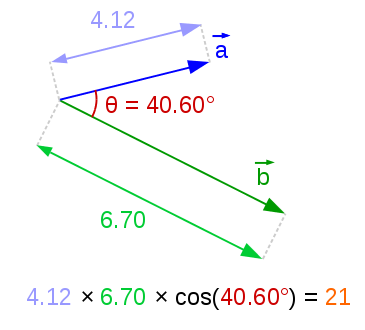
Le produit scalaire a une formule géométrique et algébrique équivalentes :
$\begin{cases} \vec{a} \cdot \vec{b} =\|\vec{a}\|\ \|\vec{b}\|\ \cos \theta \\ \vec{a} \cdot \vec{b} = a_x b_x + a_y b_y \end{cases}$

Comme cas particuliers, on a :
- Si $\theta = 90° $ alors $\cos\theta = 0 $$\implies \vec{a} \perp \vec{b} $$\implies \vec{a} \cdot \vec{b} = 0$
- Si $\theta = 0° $ alors $\cos\theta = 1$$\implies \vec{a} \parallel \vec{b} $$\implies \vec{a} \cdot \vec{b} = \|\vec{a}\|\ \|\vec{b}\|$
- Si $\theta = 180° $ alors $\cos\theta = -1$$\implies \vec{a} \parallel \vec{b} $$\implies \vec{a} \cdot \vec{b} = - \|\vec{a}\|\ \|\vec{b}\|$
- Si $\vec{a} \parallel \vec{b} $ alors $\vec{a} \cdot \vec{b} = a \cdot b$
- $\theta = 90° $$\implies \cos\theta = 0 $$\implies \vec{a} \perp \vec{b} $$\implies \vec{a} \cdot \vec{b} = 0$
- $\theta = 0° $$\implies \cos\theta = 1$$\implies \vec{a} \parallel \vec{b} $$\implies \vec{a} \cdot \vec{b} = \|\vec{a}\|\ \|\vec{b}\|$
- $\theta = 180° $$\implies \cos\theta = -1$$\implies \vec{a} \parallel \vec{b} $$\implies \vec{a} \cdot \vec{b} = - \|\vec{a}\|\ \|\vec{b}\|$
- $\vec{a} \parallel \vec{b} $$\implies \vec{a} \cdot \vec{b} = a \cdot b$
En terme moins mathématique, le produit scalaire nous dit combien ces vecteurs pointent dans le même sens, s'il nous répond $+1$, c'est qu'ils sont parfaitement alignés, $0$ correspond au cas perpendiculaire (pas du tout alignés), une valeur comme $0.7$ voudra dire entre les deux. Et finalement $-1$ veut dire aligné mais dans un sens différent.
Petite note de rigueur mathématique sur le paragraphe précédent, les valeurs de $1$ et $-1$ sont valables seulement si les vecteurs sont normés.
On peut voir facilement le produit scalaire comme une projection, quand je projette $\vec{a}$ sur $\vec{b}$, j'obtiens une longueur $a_b$ et par la définition du cosinus, $a_b = \|\vec{a}\| \cos\theta$, le produit scalaire peut donc aussi s'écrire :
$\vec{a} \cdot \vec{b} = a_b\ \|\vec{b}\| = b_a \|\vec{a}\|$

Quand un des vecteurs est normé, la norme vaut $1$ et donc le produit scalaire vaut cette projection :
$\vec{a} \cdot \vec{1}_b = a_b$
Et quand les deux vecteurs sont normés, le produit scalaire vaut le cosinus :
$\vec{1}_a \cdot \vec{1}_b = \cos\theta$
Le produit scalaire peut également être négatif, pour la définition géométrique, c'est parce que $\cos\theta < 0$ et pour la définition par la projection c'est parce que $a_b < 0$ :

Le nom de produit vient de la distributivité : $\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}$ et de l'homogénéité : $k (\vec{a} \cdot \vec{b}) = (k \vec{a}) \cdot \vec{b}$. Ces deux priorités en font par définition une transformation linéaire.
Avec les cas particuliers et la linéarité, on retrouve la formule algébrique : (clique sur le bouton pour voir le développement avec plus de détails !)
$\vec{a} \cdot \vec{b} $ $= (\color{red}{a_x \vec{1}_x} + \color{green}{a_y \vec{1}_y}) \cdot (\color{red}{b_x \vec{1}_x} + \color{green}{b_y \vec{1}_y}) $ $= \color{red}{a_x b_x} (\underbrace{\color{red}{\vec{1}_x} \cdot \color{red}{\vec{1}_x}}_{1}) $ $+ \color{red}{a_x} \color{green}{b_y} (\underbrace{\color{red}{\vec{1}_x} \cdot \color{green}{\vec{1}_y}}_{0}) $ $+ \color{green}{a_y} \color{red}{b_x} (\underbrace{\color{green}{\vec{1}_y} \cdot \color{red}{\vec{1}_x}}_{0}) $ $+ \color{green}{a_y b_y} (\underbrace{\color{green}{\vec{1}_y} \cdot \color{green}{\vec{1}_y}}_{1})$ $= \color{red}{a_x b_x} + \color{green}{a_y b_y}$
En python avec numpy, il existe la fonction numpy.dot :
from numpy import dot
dot([1,2],[3,4]) # 1*3 + 2*4 = 9
Cette opération a une interprétation physique très importante qui est la notion de travail.
Voici une vidéo montrant le rapport entre produit scalaire et travail.
Le travail et l'énergie sont des notions importantes en physique, plus d'infos sur clipedia dans la série des 4 vidéos sur l'énergie. Cependant, dans la vidéo, on était en une dimension, on avait la force $F$ et le déplacement $x$, et donc $W = F \cdot x$. En plusieurs dimensions, ce sont tous les deux des vecteurs, et on a donc le travail qui vaut $W = \vec{F} \cdot \vec{x}$, qui est un produit scalaire ! La page de physique parle avec plus de détails des forces comme vecteurs.
En anglais, le produit scalaire s'appelle scalar product ou dot product (dot voulant dire point comme dans la notation $\vec{a} \cdot \vec{b}$). Une explication du dot product en anglais est donnée sur betterexplained.
Norme 3D
Pour la 3D, les opérations de bases restent les mêmes, ce qui fait que la majorité des équations vectorielles sont aussi valides en 3D.
La norme s'étend naturellement avec pythagore en 3D : $\|\vec{v}\| = \sqrt{v_x^2 + v_y^2 + v_z^2}$
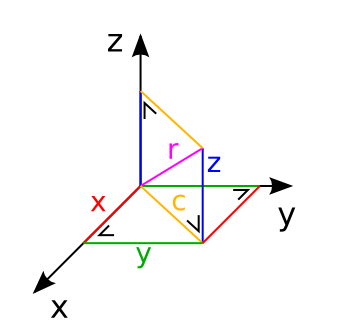
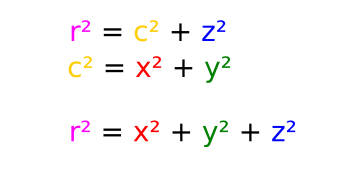
Petite remarque sur la représentation des vecteurs 3D dans le plan, on peut faire un dessin en perspective comme sur la figure précédente. Mais on peut aussi considérer un plan, comment dessiner le vecteur $\vec{1}_z = (0,0,1)$ dans le plan XY ?
Comme vous voyez sur le dessin, on représente un vecteur sortant de l'écran par un symbole $\odot$ alors qu'un vecteur rentrant dans l'écran utilise le symbole $\otimes$.
Coordonnées sphériques
Pour représenter une direction, le vecteur unitaire devient encore plus pratique. On peut également représenter une direction avec 2 angles et les coordonnées sphériques.


L'angle $\theta$ est appelée angle azimutal ou longitude et varie dans l'intervalle $[\small{0°},\small{360°}[$ ou $]-\small{180°}, +\small{180°}]$.
L'angle $\varphi$ est appelée angle zénithal ou colatitude et varie dans l'intervalle $[\small{0°},\small{180°}[$.
Attention : souvent en physique, $\theta$ est appelé $\varphi$ et $\varphi$ est appelé $\theta$ !
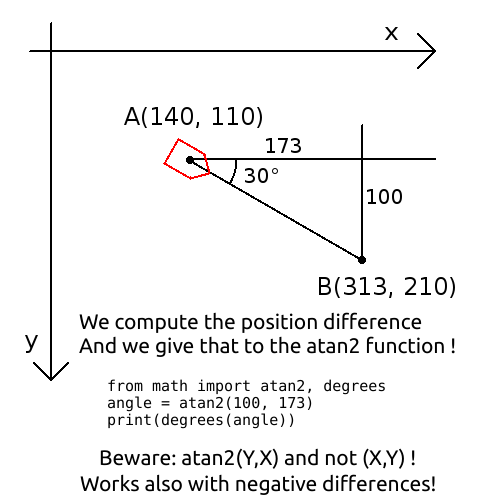
La relation inverse s'obtient via $\theta = \mathrm{atan2}(y, x)$ et $\varphi = \mathrm{acos}(z/r)$.
Produit vectoriel
Surtout utile en 3D, nous avons le produit vectoriel noté $\vec{a} \times \vec{b}$ ou $\vec{a} \wedge \vec{b}$.
C'est une opération 3D prenant deux vecteurs et renvoyant un troisième vecteur qui sera perpendiculaire aux deux vecteurs d'entrée.
Si les deux vecteurs sont parallèles, le résultat sera le vecteur nul, dans ce cas les deux vecteurs représentent la même direction ou la direction opposée.
Voici une définition du produit vectoriel :
$\vec{a} \times \vec{b}$ $= (\color{green}{a_y} \color{blue}{b_z} - \color{blue}{a_z} \color{green}{b_y} ,\ \color{blue}{a_z} \color{red}{b_x} - \color{red}{a_x} \color{blue}{b_z} ,\ \color{red}{a_x} \color{green}{b_y} - \color{green}{a_y} \color{red}{b_x})$
Un exemple: $(1,\ 2,\ 3) \times (-1,\ 1,\ 2)$ $= (1,\ -5,\ 3)$. Tu peux vérifier que $(1,\ -5,\ 3)$ est bien perpendiculaire à $(1,\ 2,\ 3)$ et $(-1,\ 1,\ 2)$ et donc normal au plan formé par $(1,\ 2,\ 3)$ et $(-1,\ 1,\ 2)$.
Si vous connaissez les déterminants, voici un moyen facile de se rappeler de la formule :
$\vec{a} \times \vec{b}$ $= \begin{vmatrix} \vec{1}_x&\vec{1}_y&\vec{1}_z\\ \color{red}{a_x}&\color{green}{a_y}&\color{blue}{a_z}\\ \color{red}{b_x}&\color{green}{b_y}&\color{blue}{b_z} \end{vmatrix}$ $= \vec{1}_x \begin{vmatrix}\color{green}{a_y}&\color{blue}{a_z}\\\color{green}{b_y}&\color{blue}{b_z}\end{vmatrix}$ $- \vec{1}_y \begin{vmatrix}\color{red}{a_x}&\color{blue}{a_z}\\\color{red}{b_x}&\color{blue}{b_z}\end{vmatrix}$ $+ \vec{1}_z \begin{vmatrix}\color{red}{a_x}&\color{green}{a_y}\\\color{red}{b_x}&\color{green}{b_y}\end{vmatrix}$ $= \vec{1}_x (\color{green}{a_y} \color{blue}{b_z} - \color{blue}{a_z} \color{green}{b_y})$ $- \vec{1}_y (\color{red}{a_x} \color{blue}{b_z} - \color{blue}{a_z} \color{red}{b_x})$ $+ \vec{1}_z (\color{red}{a_x} \color{green}{b_y} - \color{green}{a_y} \color{red}{b_x})$ $= (\color{green}{a_y} \color{blue}{b_z} - \color{blue}{a_z} \color{green}{b_y} ,\ -(\color{red}{a_x} \color{blue}{b_z - \color{blue}{a_z} \color{red}{b_x}}) ,\ \color{red}{a_x} \color{green}{b_y} - \color{green}{a_y} \color{red}{b_x})$ $= (\color{green}{a_y} \color{blue}{b_z} - \color{blue}{a_z} \color{green}{b_y} ,\ \color{blue}{a_z} \color{red}{b_x} - \color{red}{a_x} \color{blue}{b_z} ,\ \color{red}{a_x} \color{green}{b_y} - \color{green}{a_y} \color{red}{b_x})$
Si $\vec{c} = \vec{a} \times \vec{b}$ alors $c = a\ b\ \sin \theta$.
Si $\vec{c} = \vec{a} \times \vec{b} \implies c = a\ b\ \sin \theta$.
Dans notre exemple $(1,\ 2,\ 3) \times (-1,\ 1,\ 2)$ = $(1,\ -5,\ 3)$. Tu peux vérifier que la norme du vecteur résultant est bien de $a\ b\ \sin \theta$. L'angle est mesurable avec une équerre ou via le produit scalaire.
Un moyen mnémotechnique pour se rappeler du sens de $\vec{c}$ est la règle de la main droite. Vous pouvez essayer sur la figure suivante : sur votre main droite, $\vec{a}$ est votre pouce, $\vec{b}$ votre index, et $\vec{a} \times \vec{b}$ votre majeur.


Attention, si $\theta > \small{180°}$ alors $\sin \theta < 0$ et donc $\theta > \small{180°} \implies \sin \theta < 0$ $\implies$ le vecteur est opposé à la règle de la main droite.
Une autre règle de la main droite est expliquée en deux minutes dans cette vidéo (à la minute 21:40). La discussion pour $\theta > \small{180°}$ est à la minute 25:30.
Comme vu sur l'image animée précédente, si $\vec{a} \parallel \vec{b}$ alors $\sin\theta = 0$ et donc $\vec{a} \times \vec{b} = \vec{0}$. $\vec{a} \parallel \vec{b}\implies \sin\theta = 0$ $\implies \vec{a} \times \vec{b} = \vec{0}$. De même, si $\vec{a} \perp \vec{b}$ alors $\sin\theta = \pm 1$ $\vec{a} \perp \vec{b}$ $\implies \sin\theta = \pm 1$ $\implies \|\vec{a} \times \vec{b}\| = \pm\ \|\vec{a}\|\ \|\vec{b}\|$ (utilisez la règle de la main droite pour se souvenir du sens).
Si les deux vecteurs d'entrée sont de norme 1 et perpendiculaires, le vecteur résultant sera aussi de norme 1. En particulier, on a (pour un repère dextrogyre) :
$\begin{cases} \color{red}{\vec{1}_x} \times \color{green}{\vec{1}_y} = \color{blue}{\vec{1}_z} \\ \color{green}{\vec{1}_y} \times \color{blue}{\vec{1}_z} = \color{red}{\vec{1}_x} \\ \color{blue}{\vec{1}_z} \times \color{red}{\vec{1}_x} = \color{green}{\vec{1}_y} \\ \end{cases} \quad$ $\begin{cases} \color{green}{\vec{1}_y} \times \color{red}{\vec{1}_x} = - \color{blue}{\vec{1}_z} \\ \color{blue}{\vec{1}_z} \times \color{green}{\vec{1}_y} = - \color{red}{\vec{1}_x} \\ \color{red}{\vec{1}_x} \times \color{blue}{\vec{1}_z} = - \color{green}{\vec{1}_y} \\ \end{cases}$
Un moyen mnémotechnique pour se rappeler de ceci est que, si les deux vecteurs sont dans l'ordre (dans la séquence x y z x y z) alors c'est +, sinon c'est −.
Le nom de produit vient de la distributivité : $\vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}$ et de l'homogénéité : $k (\vec{a} \times \vec{b}) = (k \vec{a}) \times \vec{b}$.
Attention, le produit vectoriel est anti-commutatif : $\vec{b} \times \vec{a} = \color{red}{\mathbf{-}}\ \vec{a} \times \vec{b}$.
Avec les cas particuliers et la linéarité, on retrouve la formule : (clique sur le bouton pour voir le développement avec plus de détails !)
$\vec{a} \times \vec{b}$ $= (\color{red}{a_x} \color{red}{\vec{1}_x} + \color{green}{a_y}\ \color{green}{\vec{1}_y} + \color{blue}{a_z}\ \color{blue}{\vec{1}_z}) $$\times (\color{red}{b_x} \color{red}{\vec{1}_x} + \color{green}{b_y}\ \color{green}{\vec{1}_y} + \color{blue}{b_z}\ \color{blue}{\vec{1}_z})$
$= \color{red}{a_x} \color{red}{b_x} (\underbrace{\color{red}{\vec{1}_x} \times \color{red}{\vec{1}_x}}_{\vec{0}})$ $+ \color{red}{a_x} \color{green}{b_y} (\underbrace{\color{red}{\vec{1}_x} \times \color{green}{\vec{1}_y}}_{\color{blue}{\vec{1}_z}})$ $+ \color{red}{a_x} \color{blue}{b_z} (\underbrace{\color{red}{\vec{1}_x} \times \color{blue}{\vec{1}_z}}_{-\color{green}{\vec{1}_y}})$
$+ \color{green}{a_y} \color{red}{b_x} (\underbrace{\color{green}{\vec{1}_y} \times \color{red}{\vec{1}_x}}_{-\color{blue}{\vec{1}_z}})$ $+ \color{green}{a_y} \color{green}{b_y} (\underbrace{\color{green}{\vec{1}_y} \times \color{green}{\vec{1}_y}}_{\vec{0}})$ $+ \color{green}{a_y} \color{blue}{b_z} (\underbrace{\color{green}{\vec{1}_y} \times \color{blue}{\vec{1}_z}}_{\color{red}{\vec{1}_x}})$
$+ \color{blue}{a_z} \color{red}{b_x} (\underbrace{\color{blue}{\vec{1}_z} \times \color{red}{\vec{1}_x}}_{\color{green}{\vec{1}_y}})$ $+ \color{blue}{a_z} \color{green}{b_y} (\underbrace{\color{blue}{\vec{1}_z} \times \color{green}{\vec{1}_y}}_{-\color{red}{\vec{1}_x}})$ $+ \color{blue}{a_z} \color{blue}{b_z} (\underbrace{\color{blue}{\vec{1}_z} \times \color{blue}{\vec{1}_z}}_{\vec{0}})$
$= \color{red}{a_x} \color{green}{b_y} \color{blue}{\vec{1}_z}$ $- \color{red}{a_x} \color{blue}{b_z} \color{green}{\vec{1}_y}$ $\quad- \color{green}{a_y} \color{red}{b_x} \color{blue}{\vec{1}_z}$ $+ \color{green}{a_y} \color{blue}{b_z} \color{red}{\vec{1}_x}$ $\quad+ \color{blue}{a_z} \color{red}{b_x} \color{green}{\vec{1}_y}$ $- \color{blue}{a_z} \color{green}{b_y} \color{red}{\vec{1}_x}$
$= (\color{green}{a_y} \color{blue}{b_z} - \color{blue}{a_z} \color{green}{b_y})\color{red}{\vec{1}_x} $$+ (\ \color{blue}{a_z} \color{red}{b_x} - \color{red}{a_x} \color{blue}{b_z}) \color{green}{\vec{1}_y} $$+ (\ \color{red}{a_x} \color{green}{b_y} - \color{green}{a_y} \color{red}{b_x}) \color{blue}{\vec{1}_z}$
En python avec numpy, il existe la fonction numpy.cross :
from numpy import cross
cross([1,0,0],[0,1,0]) # array([0,0,1])
Si tu veux d'autres infos, voici les vidéos traintant du produit vectoriel sur Clipedia : [1] [2] [3]
En physique une interprétation importante du produit vectoriel est le moment de force. Plus d'infos sur Clipédia.
Équation de plan
Un plan est souvent représenté à l'aide d'un point $\vec{p}$ et une direction normale $\vec{n}$. Parfois ce vecteur est normé (on le notera alors $\vec{1}_n$), parfois non.
Remarque qu'un plan a une infinité de vecteur normal. Si $\vec{n}$ est normal (perpendiculaire) au plan, les vecteurs $2\vec{n}, -\vec{n}, -5\vec{n}$ le seront aussi ($k\ \vec{n}\quad \forall k \in \mathbb{R}_{\ne 0}$).
La distance d'un point $\vec{r}$ par rapport à un plan est alors facilement exprimable avec un produit scalaire $(\vec{r} - \vec{p}) \cdot \vec{1}_n$.
Attention, il faut prendre la valeur absolue de ce produit scalaire pour obtenir la distance, une valeur négative représente une distance de l'autre côté du vecteur $\vec{n}$.
On peut facilement définir l'équation du plan en exprimant le fait que tous les points sont à une distance 0 :
$(\vec{r} - \vec{p}) \cdot \vec{1}_n = 0$ $\iff ((\vec{r} - \vec{p}) \cdot \vec{1}_n)\ \|\vec{n}\| = 0 \|\vec{n}\|$ $\iff (\vec{r} - \vec{p}) \cdot (\vec{1}_n\ \|\vec{n}\|) = 0$ $\iff (\vec{r} - \vec{p}) \cdot \vec{n} = 0$ $\iff \vec{r} \cdot \vec{n} - \vec{p} \cdot \vec{n} = 0$ $\iff \underbrace{\vec{r}}_{(x,y,z)} \cdot \underbrace{\vec{n}}_{(a,b,c)} = \underbrace{\vec{p} \cdot \vec{n}}_{d}$ $\iff ax + by + cz = d$
Équation de droite 2D
En 2D, ce concept de vecteur normal peut être appliqué à la droite. Et donc, en 2D, une droite passant par le point $\vec{p}$, de vecteur normal $\vec{n}$ aura l'équation :
$(\vec{r} - \vec{p}) \cdot \vec{1}_n = 0$ $\iff ((\vec{r} - \vec{p}) \cdot \vec{1}_n)\ \|\vec{n}\| = 0 \|\vec{n}\|$ $\iff (\vec{r} - \vec{p}) \cdot (\vec{1}_n\ \|\vec{n}\|) = 0$ $\iff (\vec{r} - \vec{p}) \cdot \vec{n} = 0$ $\iff \vec{r} \cdot \vec{n} - \vec{p} \cdot \vec{n} = 0$ $\iff \underbrace{\vec{r}}_{(x,y)} \cdot \underbrace{\vec{n}}_{(a,b)} = \underbrace{\vec{p} \cdot \vec{n}}_{c}$ $\iff ax + by = c$
La distance point droite se calculera facilement avec le produit scalaire $(\vec{r} - \vec{p}) \cdot \vec{1}_n$ où $\vec{p}$ est un point de la droite et $\vec{r}$ est le point pour lequel on veut calculer la distance.
Nous connaissons également l'équation vectorielle de la droite en 2D : $\vec{r}(t) = \vec{p} + t \cdot \vec{d}$
Le vecteur directeur et le vecteur normal sont bien sûr perpendiculaires. Pour avoir un vecteur normal quand on a un vecteur directeur, il suffit de faire tourner le vecteur de 90°.
La formule pour faire tourner un vecteur $(x,y)$ de 90° est très simple à retenir : $R_{90°}(x,y) = (-y,x)$Et donc, on a $(n_x, n_y) = (-d_y, d_x)$
En développant les deux équations (vectorielles et carthésiennes), on obtient une équivalence :
$\vec{r}(t) = \vec{p} + t \cdot \vec{d}$ $\iff \cases{ r_x = p_x + t \cdot d_x\\ r_y = p_y + t \cdot d_y }$ $\iff \cases{ t = (r_x - p_x) / d_x \quad (1)\\ r_y = p_y + ((r_x - p_x) / d_x) \cdot d_y\quad (2) }$ $(2) \iff d_x\ r_y = p_y\ d_x + d_y\ (r_x - p_x) $ $\iff d_x\ r_y = d_x\ p_y + d_y\ r_x - d_y\ p_x$ $\iff -d_y\ r_x + d_x\ r_y = - d_y\ p_x + d_x\ p_y $ $\iff n_x\ r_x + n_y\ r_y = n_x\ p_x + n_y\ p_y$ $\iff \vec{n} \cdot \vec{r} = \vec{n} \cdot \vec{p}$ $\iff \vec{r} \cdot \vec{n} = \vec{p} \cdot \vec{n}$
Intersections 3D
Trouver l'intersection $\vec{r}$ entre un plan contenant le point $\vec{p}$, dont la normale est $\vec{n}$ et une droite contenant $\vec{a}$ de vecteur directeur $\vec{d}$ :
$\cases{\vec{r} = \vec{a} + t\ \vec{d}\\(\vec{r} - \vec{p}) \cdot \vec{n} = 0}$ $\iff (\vec{a} + t\ \vec{d} - \vec{p}) \cdot \vec{n} = 0$ $\iff ((\vec{a} - \vec{p}) + t\ \vec{d}) \cdot \vec{n} = 0$ $\iff (\vec{a} - \vec{p}) \cdot \vec{n} + t\ (\vec{d} \cdot \vec{n}) = 0$ $\iff t\ (\vec{d} \cdot \vec{n}) = -(\vec{a} - \vec{p}) \cdot \vec{n}$ $\iff t = \cfrac{(\vec{p} - \vec{a}) \cdot \vec{n}}{\vec{d} \cdot \vec{n}}$
Physique
Beaucoup d'objets physiques sont représentés par des vecteurs comme les forces, la position, la vitesse et l'accélération, jette un œil à ma page physique !
Matrices
Motivation
Nous allons voir les matrices, un élément mathématique simple pour traiter des choses linéaires. Comme par exemple les transformations en 3D. Un vaisseau en 3D par exemple peut être transformé : on peut le redimensionner, le tourner, le déplacer.
Ce chapitre et le suivant pourront répondre à des questions comme celles-ci :
J'ai un point $(2,1)$, je le tourne de $45°$, où est-il maintenant ?
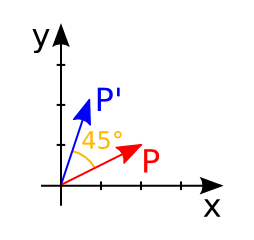
Nous verrons qu'il existe une matrice qui permet de nous donner la solution. On pourra demander à la matrice de nous calculer le nouveau point.
J'ai un point $(2,1)$, je le tourne de $45°$ et puis je le redimensionne d'un facteur $4$, je le déplace de $(-6,-4)$, puis je le tourne de $30°$, où est-il maintenant ?
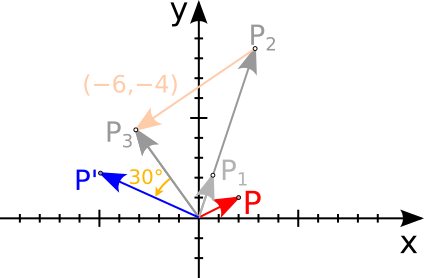
Nous verrons que pour ce problème, il existe aussi une et une seule matrice qui permet de nous donner la solution. On pourra demander à cette la matrice de nous calculer le nouveau point.
Si tu ne veux pas rentrer dans les maths, dis-toi juste qu'une matrice est une boîte magique qui transforme un point. Vois une matrice comme une transformation.
Et finalement, $(2,1)$ était en fait un des 4 sommets d'un rectangle $(\pm 2, \pm 1)$, où tomberont leurs 3 autres points après la transformation ? Sur la figure, le rectangle rouge est transformé en rectangle bleu. Vous pouvez voir les états successifs, le rectangle tourne, puis s'agrandit, puis se déplace, puis tourne encore.
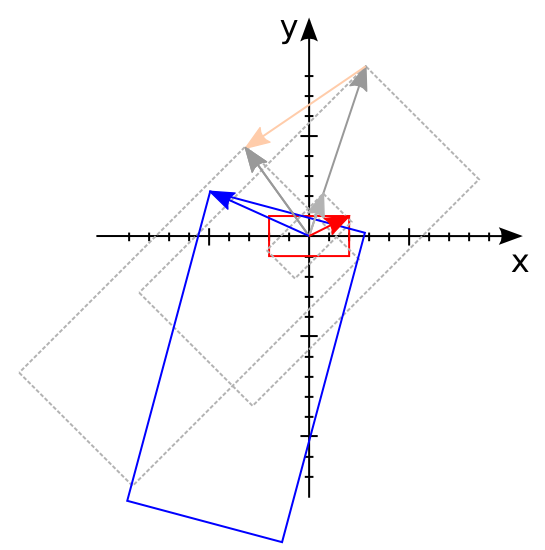
Vu que la transformation est représentée par une et une seule matrice, on pourra demander 4 fois à la matrice de nous calculer le point transformé.
Vu que les 4 points représentaient un rectangle, les 4 nouveaux points nous donne le rectangle transformé.
Définition
Une matrice, c'est un tableau de nombres avec des lignes et des colonnes. Par exemple $\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}$ est une matrice à 2 lignes et 3 colonnes, on parle alors de matrice de forme (ou de dimensions) $(2 \times 3)$ ou simplement de matrice $(2 \times 3)$. Dans la littérature anglaise, on voit souvent la notation avec des bords droits : $\begin{bmatrix}1&2&3\\4&5&6\end{bmatrix}$
Une matrice ligne est une matrice à une ligne (une $(n \times 1)$), une matrice colonne est une matrice à une colonne (une $(1 \times n)$). Une matrice carrée a autant de lignes que de colonnes (une $(n \times n)$). On peut alors parler de matrice colonne de taille 5 (une $(5 \times 1)$), de matrice ligne de taille 5 (une $(1 \times 5)$), ou de matrice carrée de taille 5 (une $(5 \times 5)$).
Quelques opérations de base sont définies de la même manière qu'avec les vecteurs :
-
L'addition :
$ \begin{pmatrix}7&14&18\\14&16&7\end{pmatrix} $
$+ \begin{pmatrix}1&1&18\\4&11&0\end{pmatrix}$
$= \begin{pmatrix}1+7&14+1&18+18\\14+4&16+11&7+0\end{pmatrix}$
$= \begin{pmatrix}8&15&36\\18&27&7\end{pmatrix}$
Les matrices doivent bien entendu être de même forme. - La multiplication par un nombre : $4 \cdot \begin{pmatrix}1&-1&18\\-4&11&0\end{pmatrix}$ $= \begin{pmatrix}4&-4&72\\-16&44&0\end{pmatrix}$
- La soustraction : $A - B = A + (-1) \cdot B$
- La division par un nombre : $A / k = A \cdot (1/k)$
La multiplication matricielle sera différente (voir plus bas).
- La transposée d'une matrice est celle obtenue en échangant les lignes et les colonnes : $\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}^T $$= \begin{pmatrix}1&4\\2&5\\3&6\end{pmatrix}$
-
Une matrice carrée est symétrique si elle est égale à sa transposée : $\forall i,j : A_{i,j} = A_{j,i}$.
Cette matrice est symétrique : $\begin{pmatrix}1&\color{green}{2}\\\color{green}{2}&3\end{pmatrix}$
Celle ci ne l'est pas : $\begin{pmatrix}1&\color{red}{2}\\\color{red}{7}&3\end{pmatrix}$
Si vous voulez voir la définition d'une matrice et du produit matriciel avec de belles couleurs dignes d'un cours de primaire, ça se passe ici ! Nous avons également notre ami betterexplained qui a un mot à dire.
Produit matriciel
Cependant, les matrices ont un concept important : le produit matriciel, noté $A \times B$, $A \cdot B$ ou $AB$.
Condition
Si $A$ est une matrice de taille $(a \times b)$ et $B$ est une matrice de taille $(c \times d)$, le produit $A \times B$ existe seulement si $b = c$. Le résultat sera alors une matrice $(a \times d)$. Par exemple, on peut multiplier une $(\color{red}{7} \times \color{green}{2})$ avec une $(\color{green}{2} \times \color{blue}{4})$ mais pas une avec une $(\color{red}{7} \times \color{green}{2})$ avec une $(\color{orange}{4} \times \color{blue}{4})$. En d'autres mots :
Pour deux matrices $A$ et $B$ : $A \times B$ existe si le nombre de colonnes de $A$ $=$ le nombre de lignes de $B$
Quand cette condition est remplie, la matrice résultante aura autant de lignes que la première matrice et autant de colonnes que la deuxième. Par exemple, une $(\color{red}{7} \times \color{green}{2})$ avec une $(\color{green}{2} \times \color{blue}{4})$ donne une $(\color{red}{7} \times \color{blue}{4})$
Une $(\color{red}{a} \times \color{green}{b})$ fois une $(\color{green}{b} \times \color{blue}{c})$ donnera une $(\color{red}{a} \times \color{blue}{c})$.
Une ligne fois une colonne
Pour avoir la matrice résultante, il faut d'abord savoir multiplier une ligne avec une colonne. de même taille. C'est la même opération que le produit scalaire.
$ \begin{pmatrix}\color{red}{x}&\color{red}{y}&\color{red}{z}\end{pmatrix} \begin{pmatrix}\color{blue}{x'}\\\color{blue}{y'}\\\color{blue}{z'}\end{pmatrix} $ $= \begin{pmatrix} \color{red}{x}\color{blue}{x'} + \color{red}{y}\color{blue}{y'} + \color{red}{z}\color{blue}{z'} \end{pmatrix} $
Une matrice $(1 \times n)$ fois une matrice $(n \times 1)$ fait donc une matrice $(1 \times 1)$ donc un seul nombre.
Par exemple, vu que $(\color{red}{1},\ \color{red}{-2},\ \color{red}{4}) \cdot (\color{blue}{7},\ \color{blue}{3},\ \color{blue}{-2}) $ $= \color{red}{1} \times \color{blue}{7} + \color{red}{(-2)} \times \color{blue}{3} + \color{red}{4} \times \color{blue}{(-2)} $ $= 7 - 6 - 8 = -8$, on a :
$ \begin{pmatrix}\color{red}{1}&\color{red}{-2}&\color{red}{4}\end{pmatrix} \begin{pmatrix}\color{blue}{7}\\\color{blue}{3}\\\color{blue}{-2}\end{pmatrix} $ $= \begin{pmatrix} \color{red}{1} \times \color{blue}{7} + (\color{red}{-2}) \times \color{blue}{3} + \color{red}{4} \times (\color{blue}{-2}) \end{pmatrix} $ $= \begin{pmatrix} 7 - 6 - 8 \end{pmatrix} $ $= \begin{pmatrix} -8 \end{pmatrix} $
Vous pouvez voir ça comme vous voulez, mais j'imagine que les deux vecteurs font deux files et quant une paire de nombre arrive au guichet, ils se multiplient et rentre se sommer dans le bâtiment...
Une matrice fois une matrice
Maintenant, pour multiplier une matrice $(a \times b)$ avec une matrice de taille $(b \times c)$, on a donc une matrice $(a \times c)$. La règle est celle-ci :
Pour avoir le nombre à la colonne i et ligne j, on multiplie la colonne i de la première matrice avec la ligne j de la deuxième.
Voici un exemple d'une matrice de taille $(2 \times 3)$ avec une matrice de taille $(3 \times 4)$. Donnant donc une matrice de taille $(2 \times 4)$
$\begin{pmatrix}1&4&-7\\0&8&-4\end{pmatrix} \begin{pmatrix}1&-2&1&7\\0&8&-4&2\\7&1&0&4\end{pmatrix}$ $= \begin{pmatrix}?&?&?&?\\?&?&?&?\end{pmatrix}$
Première ligne première colonne...
$\begin{pmatrix}\color{red}{1}&\color{red}{4}&\color{red}{-7}\\0&8&-4\end{pmatrix} \begin{pmatrix}\color{blue}{1}&-2&1&7\\\color{blue}{0}&8&-4&2\\\color{blue}{7}&1&0&4\end{pmatrix}$ $= \begin{pmatrix}\color{red}{1} \cdot \color{blue}{1} + \color{red}{4} \cdot \color{blue}{0} + \color{red}{-7} \cdot \color{blue}{7} = -48&?&?&?\\?&?&?&?\end{pmatrix}$
Première ligne deuxième colonne...
$\begin{pmatrix}\color{red}{1}&\color{red}{4}&\color{red}{-7}\\0&8&-4\end{pmatrix} \begin{pmatrix}1&\color{blue}{-2}&1&7\\0&\color{blue}{8}&-4&2\\7&\color{blue}{1}&0&4\end{pmatrix}$ $= \begin{pmatrix}-48&\color{red}{1} \cdot \color{blue}{-2} + \color{red}{4} \cdot \color{blue}{8} + \color{red}{-7} \cdot \color{blue}{1} = 23&?&?\\?&?&?&?\end{pmatrix}$
Et cetera...
$\begin{pmatrix}1&4&-7\\0&8&-4\end{pmatrix} \begin{pmatrix}1&-2&1&7\\0&8&-4&2\\7&1&0&4\end{pmatrix}$ $= \begin{pmatrix} \color{red}{1} \cdot \color{blue}{1} + \color{red}{4} \cdot \color{blue}{0} + \color{red}{-7} \cdot \color{blue}{7} & \color{red}{1} \cdot \color{blue}{-2} + \color{red}{4} \cdot \color{blue}{8} + \color{red}{-7} \cdot \color{blue}{1} & \color{red}{1} \cdot \color{blue}{1} + \color{red}{4} \cdot \color{blue}{-4} + \color{red}{-7} \cdot \color{blue}{0} & \color{red}{1} \cdot \color{blue}{7} + \color{red}{4} \cdot \color{blue}{2} + \color{red}{-7} \cdot \color{blue}{4} \\ \color{red}{0} \cdot \color{blue}{1} + \color{red}{8} \cdot \color{blue}{0} + \color{red}{-4} \cdot \color{blue}{7} & \color{red}{0} \cdot \color{blue}{-2} + \color{red}{8} \cdot \color{blue}{8} + \color{red}{-4} \cdot \color{blue}{1} & \color{red}{0} \cdot \color{blue}{1} + \color{red}{8} \cdot \color{blue}{-4} + \color{red}{-4} \cdot \color{blue}{0} & \color{red}{0} \cdot \color{blue}{7} + \color{red}{8} \cdot \color{blue}{2} + \color{red}{-4} \cdot \color{blue}{4} \end{pmatrix}$ $= \begin{pmatrix}-48&23&-15&-13\\-28&60&-32&0\end{pmatrix}$
Cette opération sera bien sûr effectuée par des calculettes adaptée, python est bien sûr adapté mais si vous avez la flemme d'ouvrir un terminal python (honte à vous ou lisez mon tutoriel sur la calculette python), on peut trouver des calculettes en ligne.
Dans le cas où la condition de multiplication est respectée (colonne de l'une = lignes de l'autre), le produit matriciel a quelques propriétés :
- Le produit matriciel n'est pas commutatif. Donc $\exists A,B : AB \neq BA$.
- Le produit matriciel est associatif : $ABC = (AB)C = A(BC)$.
- Le produit matriciel est distributif : $A(B + C) = AB + AC$.
Transformations
Code python
En informatique 3D, on manipule surtout des matrices colonnes de taille 2, 3 ou 4 et des matrices carrées de même taille.
Un point est souvent représenté avec une matrice colonne, par exemple en 2D, le point $(1,\ 2)$ sera souvent représenté $\begin{pmatrix}1\\2\end{pmatrix}$.
En python, une manière simple de manipuler des matrices et des vecteurs est la bibliothèque numpy.
Soit on utilise la classe générique numpy.array (méthode que je recommande) :
from numpy import array
P = array([1,2]) # Un vecteur 2D
M = array([[5,6],[7,8]]) # Une matrice carrée 2x2
G = array([[1,1],[9,0]]) # Une autre matrice carrée 2x2
Q = 2 * P # multiplication par un nombre
R = P + R # addition vectorielle/matricielle
S = M.dot(P) # multiplication matricielle, S est un vecteur
S = M @ P # multiplication matricielle, Python 3.5 uniquement
H = M.dot(G) # Une 2x2 fois une 2x2 donne une 2x2
H = M @ G # multiplication matricielle, Python 3.5 uniquement
T = M.T # T est la transposée de M
a = M[0][1] # lire les éléments d'une matrice, ici première ligne, deuxième colonne
x = P[0] # lire les 2 composantes du vecteur comme ...
y = P[1] # ... ceci
x,y = P # Raccourci pour la lecture d'un vecteur
(a,b),(c,d) = M # Raccourci pour la lecture d'une matrice
print(P.size) # 2 éléments
print(P.shape) # (2,) une dimension de taille 2
print(M.size) # 4 éléments
print(M.shape) # (2,2) deux dimensions, shape = (2 x 2)
Soit la classe numpy.matrix :
from numpy import matrix
P = matrix([[1],[2]]) # Une matrice colonne de taille 2
M = matrix([[5,6],[7,8]]) # Une matrice carrée 2x2
M = matrix('5 6; 7 8') # Version allégée, pratique pour utiliser python comme calculette
G = matrix([[1,1],[9,0]]) # Une autre matrice carrée 2x2
Q = 2 * P # multiplication par un nombre
R = P + R # addition vectorielle/matricielle
S = M * P # multiplication matricielle, S est une une matrice colonne
S = M @ P # multiplication matricielle, Python 3.5 uniquement
H = M * G # Une 2x2 fois une 2x2 donne une 2x2
H = M @ G # multiplication matricielle, Python 3.5 uniquement
T = M.T # T est la transposée de M
a = M[0,1] # lire les éléments d'une matrice, ici première ligne, deuxième colonne
x = P[0,0] # lire les 2 composantes de la matrice comme ...
y = P[1,0] # ... ceci
print(P.size) # 2 éléments
print(P.shape) # (2,1) en deux dimensions shape = (2 x 1)
print(M.size) # 4 éléments
print(M.shape) # (2,2) en deux dimensions shape = (2 x 2)
Faites donc attention à l'opérateur * (et **) qui n'a pas la même sémantique dans les deux cas :
A = array([[1,2],[3,4]]) * array([[1,2],[3,4]]) # [[1*1, 2*2], [3*3, 4*4]]
B = matrix([[1,2],[3,4]]) * matrix([[1,2],[3,4]]) # [[1*1+2*3, 1*2+2*4], [3*1+4*3, 3*2+4*4]]
C = array([[1,2],[3,4]]) ** array([[1,2],[3,4]]) # [[1**1,2**2],[3**3,4**4]]
D = array([[1,2],[3,4]]) ** 2 # [[1**2,2**2],[3**2,4**2]]
B = matrix([[1,2],[3,4]]) ** 2 # [[1*1+2*3, 1*2+2*4], [3*1+4*3, 3*2+4*4]]
En Python 3.5, veuillez utiliser l'opérateur @ pour toutes vos multiplications de matrices.
Beaucoup d'opérations qui marchent sur les nombres ont une version numpy qui marche avec les array et parfois matrix :
A = array([4,5]) + 3 # array([5,6])
A = array([4,5]) ** 2 # array([4**2, 5**2])
numpy.cos(array([1,2,3])) # array([cos(1),cos(2),cos(3)])
Si vous connaissez les déterminants et les inversions de matrice, ça se passe dans numpy.linalg :
from numpy.linalg import det, inv
M = matrix('1 2; 3 4')
A = array([[1,2], [3,4]])
d = det(M) # -2.0 fast because it uses LU decomposition and LAPACK
d = det(A) # -2.0
I = inv(M) # inverse matrix: matrix('-2 1; 1.5 -0.5')
I = inv(A) # inverse matrix: array([[-2, 1], [1.5, -0.5]])
I = M ** -1 # matrix does understand negative matrix exponent
Système d'équation et matrice
En informatique 3D, on manipule surtout des matrices colonnes de taille 2, 3 ou 4 et des matrices carrées de même taille.
Un point est souvent représenté avec une matrice colonne, par exemple en 2D, le point $(1,\ 2)$ sera souvent représenté $\begin{pmatrix}1\\2\end{pmatrix}$.
Une transformation 2D linéaire sera représentée par une matrice $(2 \times 2)$. Si on multiple une telle matrice par un point, on obtient un autre point. En effet, une matrice de taille $(2 \times 2)$ avec une matrice de taille $(2 \times 1)$ fait une matrice de taille $(2 \times 1)$.
Donc en général, si on a une matrice $M = \begin{pmatrix}a&b\\c&d\end{pmatrix}$ et un point $P = \begin{pmatrix}x\\y\end{pmatrix}$, on s'intéressera au point $P' = \begin{pmatrix}x'\\y'\end{pmatrix}$. La matrice représente une transformation, il suffit de multiplier $M$ par $P$ pour avoir $P'$.
$P' = MP$ $\iff \begin{pmatrix}x'\\y'\end{pmatrix} = \begin{pmatrix}\color{red}a&\color{red}b\\\color{blue}c&\color{blue}d\end{pmatrix} \begin{pmatrix}x\\y\end{pmatrix}$ $\iff \begin{cases}x' = \color{red}{a}\ x + \color{red}{b}\ y\\y' = \color{blue}{c}\ x + \color{blue}{d}\ y\end{cases}$
Trois représentations équivalentes de la transformation $P' = MP$.
En termes plus mathématiques, une matrice peut représenter toute transformation linéaire. Pour savoir ce qu'est une transformation linéaire, clique sur le bouton suivant, sinon passe à la suite.
¶Une transformation $T$ est linéaire si $\forall\ \vec{a}, \vec{b}, k:$
- $T(\vec{a} + \vec{b}) = T(\vec{a}) + T(\vec{b})$
- $T(k\ \vec{a}) = k\ T(\vec{a})$
Une transformation possédant la première propriété est dite additive, et, pour la seconde, homogène.
Par exemple $T(\vec{v}) = 2 \cdot \vec{v}$ ou $T(\vec{v}) = (v_y, -v_x)$ sont linéaires mais $T(\vec{v}) = \vec{v} + (1,0)$ ne l'est pas, remplacez $T$ dans la définition et vous verrez quand les égalités sont respectées.
$T(\vec{v}) \equiv 2 \cdot \vec{v}$ $= (2\ v_x, 2\ v_y)$
$\implies \forall \vec{a}, \vec{b} : T(\vec{a} + \vec{b})$ $= 2 \cdot ((a_x + b_x, a_y + b_y))$ $= (2 a_x + 2 b_x, 2 a_y + 2 b_y)$ $= (2 a_x, 2 a_y) + (2 b_x + 2 b_y)$ $= (2 a_x, 2 a_y) + (2 b_x + 2 b_y)$ $= T(\vec{a}) + T(\vec{b})$
$\implies \forall \vec{a}, k : T(k\ \vec{a}) $ $= 2 \cdot (k \cdot (v_x, v_y))$ $= 2 \cdot (k\ v_x, k\ v_y)$ $= (2\ k\ v_x, 2\ k\ v_y)$ $= k\ (2\ v_x, 2\ v_y)$ $= k\ T(\vec{v})$
$T(\vec{v}) \equiv (v_y, -v_x)$
$\implies \forall \vec{a}, \vec{b} : T(\vec{a} + \vec{b})$ $= (a_y + b_y, -(a_x + b_x))$ $= (a_y + b_y, -a_x - b_x)$ $= (a_y + b_y, -a_x - b_x)$ $= (a_y, -a_x) + (b_y, -b_x)$ $= T(\vec{a}) + T(\vec{b})$
$\implies \forall \vec{a}, k : T(k\ \vec{v}) $ $= (k v_y, - k v_x)$ $= k\ (v_y, - v_x)$ $= k\ T(\vec{v})$
$T(\vec{v}) \equiv \vec{v} + (1, 0)$
$\implies \forall \vec{a}, \vec{b} : T(\vec{a} + \vec{b})$ $= (\vec{a} + \vec{b}) + (1, 0)$ $\neq T(\vec{a}) + T(\vec{b})$ $= \vec{a} + (1, 0) + \vec{b} + (1,0)$ $= (\vec{a} + \vec{b}) + (2, 0)$
$\implies \forall \vec{a}, k : T(k\ \vec{v}) $ $= k\ \vec{v} + (1, 0)$ $\neq k\ T(\vec{v})$ $= k\ (\vec{v} + (1,0))$ $= k\ \vec{v} + (k,0)$
Une petite remarque sur la structure d'une matrice de transformation, la première colonne représente en fait les coordonnées du vecteur $\vec{1}_x$ transformé.
$ \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix} \times \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} a \\ c \end{pmatrix} $
De la même manière, la deuxième colonne représente les coordonnées du vecteur $\vec{1}_y$
$ \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix} \times \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} b \\ d \end{pmatrix} $
On peut donc retrouver la matrice d'une transformation linéaire en calculant les coordonnées de la transformation de chaque vecteur de base.
Identité
Quelle est la matrice qui ne change pas un point ? On part d'un point $P$, on le transforme via $M$, et on obtient le même $P$. On cherche donc $M$ tel quel $P = MP$ pour tout $P$.
On part de la définition en équation, vers la notation matricielle :
$\begin{cases}x' = x\\y' = y\end{cases}$ $\iff \begin{cases}x' = \color{red}1\cdot x + \color{red}0 \cdot y\\y' = \color{blue}0 \cdot x + \color{blue}1 \cdot y\end{cases}$ $\iff \begin{pmatrix}x'\\y'\end{pmatrix} = \underbrace{\begin{pmatrix}\color{red}1&\color{red}0\\\color{blue}0&\color{blue}1\end{pmatrix}}_{I} \begin{pmatrix}x\\y\end{pmatrix}$
On appelle cette matrice matrice unité, on la note $I$, ou $I_2$ pour spécifier qu'elle est de taille 2.
Pour toute matrice carrée $M$ de n'importe quelle dimension, on a $MI = IM = M$.
Redimensionnement
Le redimensionnement, ou scale en anglais, ou homothétie en terme plus mathématique, permet de redimensionner un objet. Prenons un rectangle de côtés 2 et 3 centré en l'origine. On peut appliquer une transformation de ses points pour qu'il devienne 3 fois plus grand (transformation en bleu sur la figure) ou une transformation pour qu'il devienne 2 fois plus petit (transformation en vert sur la figure).
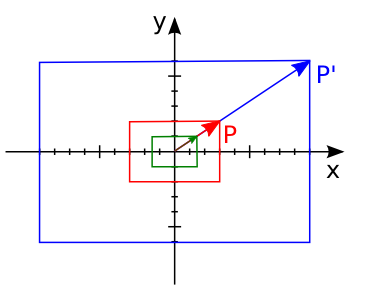
Le vecteur correspondant à ses points sera multiplié par un certain facteur $k$, dans notre exemple $k = 3$.
On se rappelera que $2$ fois plus petit, c'est $1/2$ fois plus grand.
$\cases{x' = k x\\y' = k y}$ $\iff \cases{x' = \color{red}{k}\cdot x + \color{red}{0} \cdot y\\y' = \color{blue}{k} \cdot x + \color{blue}{k} \cdot y}$ $\iff \begin{pmatrix}x'\\y'\end{pmatrix} = \begin{pmatrix}\color{red}{k}&\color{red}{0}\\\color{blue}{0}&\color{blue}{k}\end{pmatrix} \begin{pmatrix}x\\y\end{pmatrix}$
On a donc, en toute généralité pour un facteur $k$ :
$S_k = \begin{pmatrix}k&0\\0&k\end{pmatrix}$
On peut également avoir un facteur différent en $x$ et $y$, par exemple si $k_x = 2, k_y = 3$ un carré de côté $2$ centré en $(0,0)$ deviendra un rectangle de dimension $(4,6)$ centré en $(0,0)$.
Des facteurs de k négatifs sont également possible, si $k = -1$ la transformation retourne le modèle sans changer sa taille, si $k_x = 1, k_y = -1$, on fait une transformation mirroir par rapport à l'axe $x$ et dans ce cas un M deviendrait un W.
$S_\vec{k} = \begin{pmatrix}k_x&0\\0&k_y\end{pmatrix}$
Rotation
J'ai un point ou un vecteur $P = (2,1)$, et je le tourne de $\theta = 50°$ :
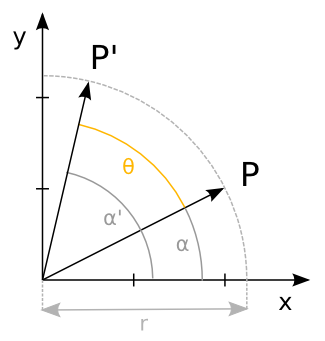
En utilisant la trigonométrie de base et la formule d'addition des sinus et des cosinus, on obtient : (clique sur le bouton pour voir le développement avec plus de détails !)
$\begin{cases}x = r\ \cos\alpha\\y = r\ \sin\alpha \\ x' = r\ \cos\alpha'\\y' = r\ \sin\alpha' \\ \alpha' = \alpha + \theta\end{cases}$ $\iff \begin{cases}x = r\ \cos\alpha\\y = r\ \sin\alpha \\ x' = r\ \cos(\alpha + \theta)\\ y' = r\ \sin(\alpha + \theta)\end{cases}$ $\iff \begin{cases}x = r\ \cos\alpha\\y = r\ \sin\alpha \\ x' = r\ (\cos\alpha\ \cos\theta - \sin\alpha\ \sin\theta)\\ y' = r\ (\cos\alpha\ \sin\theta + \sin\alpha\ \cos\theta)\end{cases}$ $\iff \begin{cases}x = r\ \cos\alpha\\y = r\ \sin\alpha \\ x' = (r\ \cos\alpha)\ \cos\theta - (r\ \sin\alpha)\ \sin\theta \\ y' = (r\ \cos\alpha)\ \sin\theta + (r\ \sin\alpha)\ \cos\theta\end{cases}$ $\iff \begin{cases}x' = x\ \cos\theta - y\ \sin\theta\\ y' = x\ \sin\theta + y\ \cos\theta\end{cases}$ $\iff \begin{cases}x' = \color{red}{\cos\theta}\cdot x \color{red}{- \sin\theta}\cdot y\\y' = \color{blue}{\sin\theta}\cdot x + \color{blue}{\cos\theta}\cdot y\end{cases}$ $\iff \begin{pmatrix}x'\\y'\end{pmatrix} = \begin{pmatrix}\color{red}{\cos\theta}& \color{red}{- \sin\theta} \\\color{blue}{\sin\theta}& \color{blue}{\cos\theta}\end{pmatrix} \begin{pmatrix}x\\y\end{pmatrix}$
On a donc, en toute généralité pour un angle $\theta$ :
$R_\theta = \begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}$
Pour notre exemple, la rotation du vecteur $(2,1)$ de $45°$ vaut :
$\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix} \begin{pmatrix}2\\1\end{pmatrix}$ $\simeq \begin{pmatrix}0.707&-0.707\\0.707&0.707\end{pmatrix} \begin{pmatrix}2\\1\end{pmatrix}$ $= \begin{pmatrix}0.70\\2.12\end{pmatrix}$
Cela marche également pour $\theta < 0$, une rotation de $-50°$, c'est une rotation de $50°$ dans l'autre sens.
En utilisant la structure d'une matrice de transformation et en sachant que la rotation est linéaire, on aurait aussi pu se demander les coordonnées de la transformation de $\vec{1}_x$ et $\vec{1}_y$.
Dessine un dessin pour voir que en effet que $\vec{1}_x$ est envoyé sur les coordonnées $(\cos\theta,\ \sin\theta)$ et que $\vec{1}_y$ est envoyé sur $(-\sin\theta,\ \cos\theta)$
Translation et coordonnées homogènes
J'ai un point en $(1,2)$ et je le déplace d'un vecteur $\vec{t} = (4,2)$
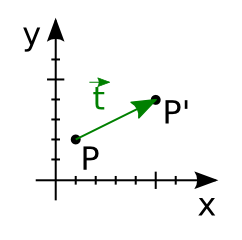
Notre équation est donc :
$\cases{x' = x + 4\\y' = y + 2}$
Cependant, ce n'est pas une transformation représentable par une matrice. En terme technique on dit qu'elle n'est pas linéaire (voir plus haut pour la définition). Mais on remarque ceci :
$\cases{x' = \color{red}{1} \cdot x + \color{red}{0} \cdot y + \color{red}{4} \cdot 1\\y' = \color{blue}{1} \cdot x + \color{blue}{0} \cdot y + \color{blue}{2} \cdot 1}$
Ceci a l'air linéaire, mais avec une dimension en plus. On va donc représenter nos points avec 3 composantes, dont la dernière vaut 1.
$ P = \begin{pmatrix}x\\y\\w = 1\end{pmatrix} \quad $;$\quad P' = \begin{pmatrix}x'\\y'\\w' = 1\end{pmatrix} $
$\cases{x' = \color{red}{1} \cdot x + \color{red}{0} \cdot y + \color{red}{4} \cdot w\\y' = \color{blue}{1} \cdot x + \color{blue}{0} \cdot y + \color{blue}{2} \cdot w\\w' = \color{black}{0} \cdot x + \color{black}{0} \cdot y + \color{black}{1} \cdot w}$ $\iff \begin{pmatrix}x'\\y'\\w'\end{pmatrix} = \begin{pmatrix}\color{red}1&\color{red}0&\color{red}4\\\color{blue}0&\color{blue}1&\color{blue}2\\\color{black}0&0&1\end{pmatrix} \begin{pmatrix}x\\y\\w\end{pmatrix}$
Les coordonnées $(x,y,w)$ d'un point $(x,y)$ sont appelées ses coordonnées homogènes.
En toute généralité, pour une translation d'un vecteur $\vec{t}$ on a :
$T_\vec{t} = \begin{pmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{pmatrix}$
Je ne vais pas rentrer dans les détails des coordonnées homogènes, mais sachez que si $w \neq 1$, on peut diviser les trois composantes par $w$ pour obtenir le point. Ainsi $(4,2,1)$, $(8,4,2)$ et $(-4,-2,-1)$ représentent tous le même point $(4,2)$. De plus si $w = 0$, on parlera de point à l'infini dans la direction $(x,y)$.
Séquence de transformations
En 2D, on va donc représenter un point avec 3 composantes, dont la dernière vaut 1. En suite on a ces matrices de redimensionnement, rotation et translation.
$ S_\vec{k} = \begin{pmatrix}k_x&0&0\\0&k_y&0\\0&0&1\end{pmatrix} \quad $;$\quad R_\theta = \begin{pmatrix}\cos\theta&-\sin\theta&0\\\sin\theta&\cos\theta&0\\0&0&1\end{pmatrix} \quad $;$\quad T_\vec{t} = \begin{pmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{pmatrix} $
Nous pouvons maintenant, résoudre l'exemple donné au début !
J'ai un point (2,1), je le tourne de 45° et puis je le redimensionne d'un facteur 4, je le déplace de (−6,−4), puis je le tourne de 30°, où est-il maintenant ?

On représente le point $(\color{red}{2},\color{blue}1)$ avec $P = \begin{pmatrix}\color{red}2\\\color{blue}1\\\color{black}1\end{pmatrix}$.
On a $P_1 = R_{45°}\times P$ pour la première transformation, puis on continue, en appliquant à chaque fois sur le point reçu précédemment.
$\begin{cases} P_1 = R_{45°}\times P \\ P_2 = S_4\times P_1 \\ P_3 = T_{(-6,-4)}\times P_2 \\ P' = R_{30°}\times P_3 \\ \end{cases} $
$\iff P' = R_{30°}\times (T_{(-6,-4)}\times P_2)$
$\iff P' = R_{30°}\times (T_{(-6,-4)}\times (S_4\times P_1))$
$\iff$ $P' = R_{30°}\times (T_{(-6,-4)}\times (S_4\times (R_{45°}\times P)))$
Et grâce à l'associativité, on peut mettre tout ça dans une seule matrice !
$P' = \underbrace{(R_{30°}\times T_{(-6,-4)}\times S_4\times R_{45°})}_{M}\times P$
Voici les valeurs numériques :
$S_4 = \begin{pmatrix}4&0&0\\0&4&0\\0&0&1\end{pmatrix}$
$R_{45°} $ $= \begin{pmatrix}\cos{45°}&-\sin{45°}&0\\\sin{45°}&\cos{45°}&0\\0&0&1\end{pmatrix} $ $\simeq \begin{pmatrix}0.707&-0.707&0\\0.707&0.707&0\\0&0&1\end{pmatrix}$
$T_{(-6,-4)} = \begin{pmatrix}1&0&-6\\0&1&-4\\0&0&1\end{pmatrix}$
$R_{30°} $ $= \begin{pmatrix}\cos{30°}&-\sin{30°}&0\\\sin{30°}&\cos{30°}&0\\0&0&1\end{pmatrix} $ $\simeq \begin{pmatrix}0.866&-0.500&0\\0.500&0.866&0\\0&0&1\end{pmatrix}$
$M = \begin{pmatrix}1.035&-3.863&-3.196\\3.863&1.035&-6.464\\0&0&1\end{pmatrix}$
$P' = \begin{pmatrix}-4.989\\2.298\\1\end{pmatrix}$
Le point $(1,2)$ est donc transformé en $(-4.989,\ 2.298)$.
Et si on a un autre point avec la même transformation ? On peut réutiliser la même matrice !
Par exemple, le rectangle $R = ((2,1), (2,-1), (-2,-1), (-2,1))$ sera transformé de la même manière.
$\begin{cases} R_1' = M R_1 = (-4.989,\ 2.298) \\ R_2' = M R_2 = (2.738,\ 0.228) \\ R_3' = M R_3 = (-1.403,\ -15.226) \\ R_4' = M R_4 = (-9.130,\ -13.156) \end{cases}$

En pratique, on aura plus que 4 points, et la carte graphique s'occupe de la multiplication de matrice en grande quantité, regardez comme les modèles suivants ont un nombre élevé de points !

Petit exercice de matrices, quelle est la matrice de rotation autour d'un point autre que $(0,0)$ ?
Si $\vec{c}$ est le centre de rotation et $\theta$ l'angle :
$M = T_{\vec{c}} \times R_{\theta} \times T_{-\vec{c}}$
Repères
[Section en création]
En 3D
En 3D, nous utiliserons donc 4 composantes $\begin{pmatrix}x\\y\\z\\w = 1\end{pmatrix}$ et des matrices $(4 \times 4)$, les rotations se feront autour d'un axe, on a donc 3 matrices de rotation élémentaires : $R_{x,\theta}, R_{y,\theta}, R_{z,\theta}$
$ S_\vec{k} = \begin{pmatrix}k_x&0&0&0\\0&k_y&0&0\\0&0&k_z&0\\0&0&0&1\end{pmatrix} ;\quad$$\ T_\vec{t} = \begin{pmatrix}1&0&0&t_x\\0&1&0&t_y\\0&0&1&t_z\\0&0&0&1\end{pmatrix} ;\quad $$ R_{x,\theta} = \begin{pmatrix}1&0&0&0\\0&\cos\theta&-\sin\theta&0\\0&\sin\theta&\cos\theta&0\\0&0&0&1\end{pmatrix} ;\quad $$ R_{y,\theta} = \begin{pmatrix}\cos\theta&0&\sin\theta&0\\0&1&0&0\\-\sin\theta&0&\cos\theta&0\\0&0&0&1\end{pmatrix} ;\quad $$ R_{z,\theta} = \begin{pmatrix}\cos\theta&-\sin\theta&0&0\\\sin\theta&\cos\theta&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix} $
On peut aussi définir la rotation autour d'un axe quelquonque $\vec{A} = (A_x, A_y, A_z)$
(RotationMatrix dans vecutils).
En utilisant les variables $c, k, s, x, y, z$ pour simplifier les notations, on a :
$ \begin{cases} c = \cos\theta \\ k = 1-c \\ s = \sin\theta \\ (x,y,z) = \vec{1}_A = \vec{A} / \|A\| \end{cases} $
$\implies R_{\vec{A},\theta} = \begin{pmatrix} c + x^2 k & x y k - z s & x z k + y s & 0 \\ y x k + z s & c + y^2k & y z k - x s & 0 \\ z x k - y s & z y k + x s & c + z^2k & 0 \\0&0&0&1 \end{pmatrix}$
Ou sous une forme plus compacte, la matrice $(3 \times 3)$ est donnée via la formule ci-dessous, les autres lignes étant mises à 0 et 1, attention cette formule marche si $\vec{A}$ est normé :
$R_{\vec{A},\theta} = (\cos\theta)\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix} $$+ (1-\cos\theta)\begin{pmatrix}x^2&x y&x z\\x y&y^2&y z\\x z&y z&z^2\end{pmatrix} $$+ \ (\sin\theta)\begin{pmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{pmatrix}$
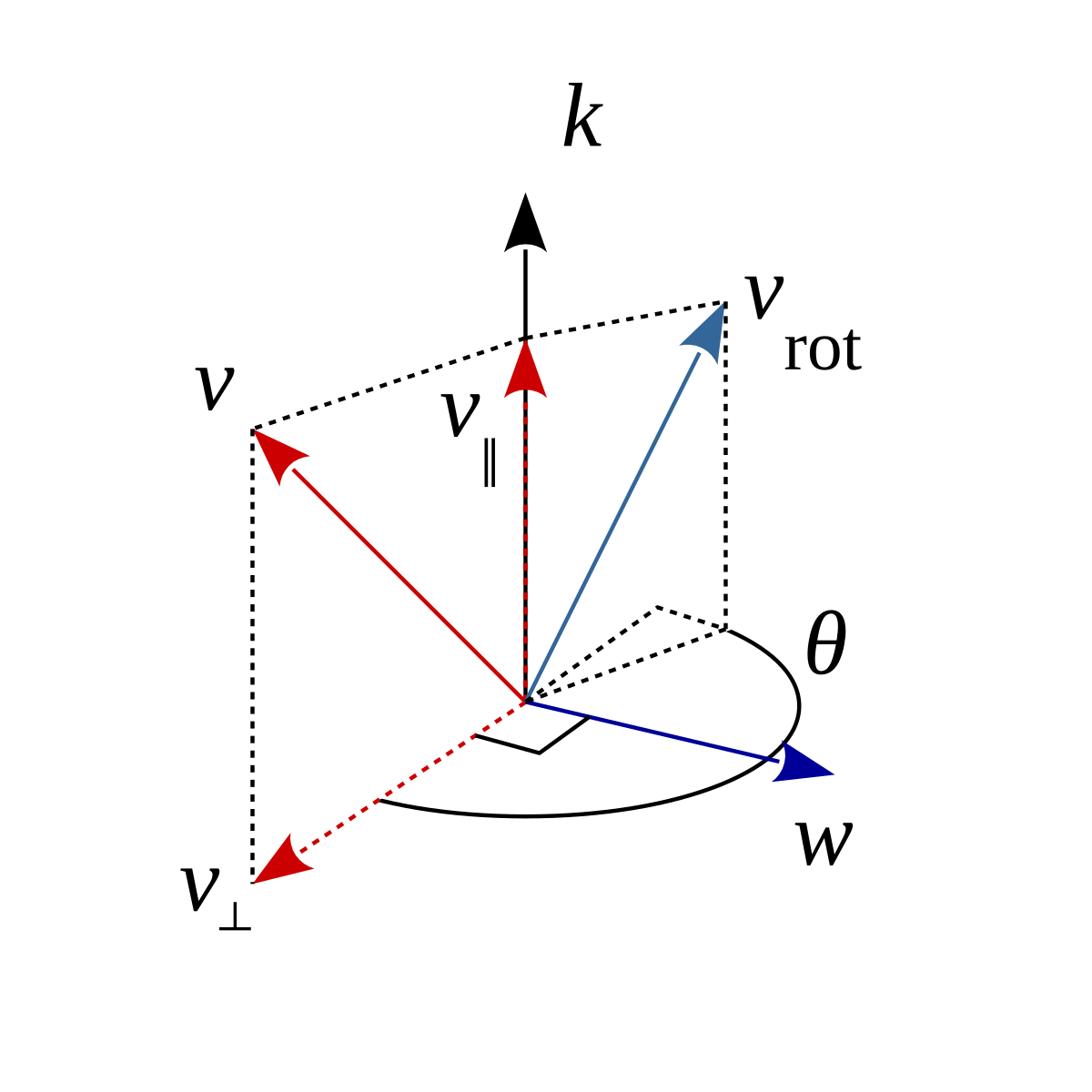
C'est la formule de Rodriguez, j'ai dû la redémontrer à un examen, très belle application des vecteurs.
 Français ici !
Français ici !